Python 時間序列建模:用指數(shù)平滑法預(yù)測股價走勢

指數(shù)平滑方法適用于非平穩(wěn)數(shù)據(jù)(即具有趨勢和/或季節(jié)性的數(shù)據(jù)),其工作方式類似于指數(shù)移動平均線。預(yù)測是過去觀察的加權(quán)平均值。這些模型更加強(qiáng)調(diào)最近的觀察結(jié)果,因為權(quán)重隨時間呈指數(shù)級變小。平滑方法很受歡迎,因為它們速度快(不需要大量計算)并且在預(yù)測方面相對可靠。(掃描本文最下方二維碼獲取全部完整源碼和Jupyter Notebook 文件打包下載。)
簡單指數(shù)平滑法:
Simple Exponential Smoothing,最基本的模型稱為簡單指數(shù)平滑(SES)。這類模型最適用于所考慮的時間序列不表現(xiàn)出任何趨勢或季節(jié)性的情況。它們也適用于只有幾個數(shù)據(jù)點的系列。
該模型通過平滑參數(shù) α 進(jìn)行參數(shù)化,其值介于 0 和 1 之間。值越高,對最近觀察的權(quán)重就越大。當(dāng) α = 0 時,對未來的預(yù)測等于歷史數(shù)據(jù)(模型擬合的數(shù)據(jù))的平均值。當(dāng) α = 1 時,所有預(yù)測值都與訓(xùn)練數(shù)據(jù)中的最后一個觀察值相同。
簡單指數(shù)平滑的預(yù)測函數(shù)是平坦的,即所有的預(yù)測,無論時間跨度如何,都等于同一個值——最后一個級別的分量。這就是為什么這種方法只適用于既沒有趨勢也沒有季節(jié)性的序列。
二次指數(shù)平滑法:
Holt 的模型是簡單指數(shù)平滑(SES)的擴(kuò)展,它通過將趨勢分量添加到模型規(guī)范中來說明序列中的趨勢。當(dāng)數(shù)據(jù)存在趨勢但沒有季節(jié)性時,應(yīng)使用此模型。
Holt 模型的一個問題是趨勢在未來是恒定的,這意味著它會無限增加/減少。這就是模型的擴(kuò)展通過添加阻尼參數(shù) φ 來抑制趨勢的原因。它使趨勢在未來收斂到一個恒定值,從而有效地將其拉平。Hyndman 和 Athanasopoulos (2018) 指出 φ 很少小于 0.8,因為阻尼對較小的 φ 值具有非常強(qiáng)的影響。
最佳做法是限制 φ 的值,使其介于 0.8 和 0.98 之間,因為對于 φ = 1,阻尼模型等效于沒有阻尼的模型。
在本文中,我們將向您展示如何將平滑方法應(yīng)用于 Google 的每月股票價格(具有趨勢且沒有明顯季節(jié)性的非平穩(wěn)數(shù)據(jù))。我們將模型與 2010-2017 年的價格進(jìn)行擬合,并對 2018 年進(jìn)行預(yù)測。
準(zhǔn)備
在下文中,我們將在相同的圖上繪制多條線,每條線代表不同模型的類型。這就是為什么我們要確保這些線條清晰可辨,尤其是黑白線條。出于這個原因,我們將為繪圖使用不同的調(diào)色板,即cubehelix:
plt.set_cmap('cubehelix')sns.set_palette('cubehelix')COLORS = [plt.cm.cubehelix(x) for x in [0.1, 0.3, 0.5, 0.7]]
步驟
執(zhí)行以下步驟以使用指數(shù)平滑方法來創(chuàng)建對 Google 股票價格的預(yù)測。
1、導(dǎo)入第三方庫:
import pandas as pdimport numpy as npimport yfinance as yffrom datetime import datefrom statsmodels.tsa.holtwinters import (ExponentialSmoothing,SimpleExpSmoothing,Holt)
2、下載調(diào)整后的谷歌股價數(shù)據(jù):
df = yf.download('GOOG',start='2010-01-01',end='2018-12-31',adjusted=True,progress=False)print(f'Downloaded {df.shape[0]} rows of data.')
3、匯總到每月頻率:
goog = df.resample('M') \.last() \.rename(columns={'Adj Close': 'adj_close'}) \.adj_close
4、創(chuàng)建訓(xùn)練/測試集
train_indices = goog.index.year < 2018goog_train = goog[train_indices]goog_test = goog[~train_indices]test_length = len(goog_test)
5、繪制價格走勢圖
goog.plot(title="Google's Stock Price")plt.tight_layout()#plt.savefig('images/ch3_im14.png')plt.show()
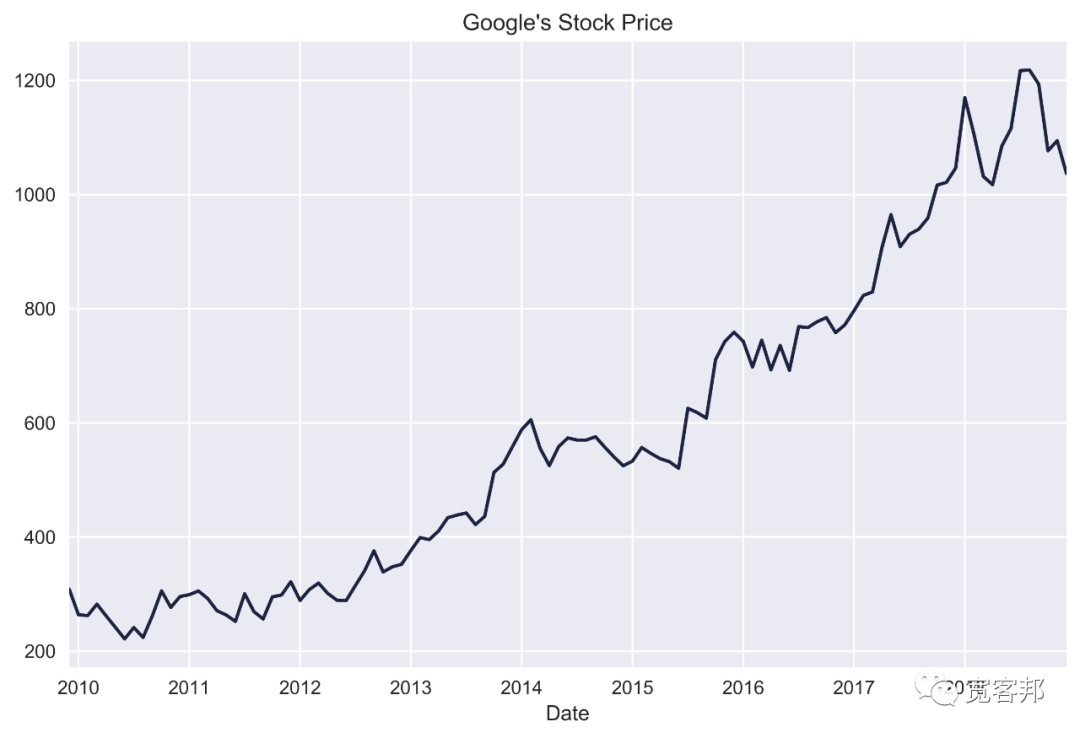
6、擬合三個簡單指數(shù)平滑(SES)模型并為它們創(chuàng)建預(yù)測:
ses_1 = SimpleExpSmoothing(goog_train).fit(smoothing_level=0.2)ses_forecast_1 = ses_1.forecast(test_length)ses_2 = SimpleExpSmoothing(goog_train).fit(smoothing_level=0.5)ses_forecast_2 = ses_2.forecast(test_length)ses_3 = SimpleExpSmoothing(goog_train).fit()alpha = ses_3.model.params['smoothing_level']ses_forecast_3 = ses_3.forecast(test_length)
7、繪制原始價格和模型的結(jié)果:
goog.plot(color=COLORS[0],title='Simple Exponential Smoothing',label='Actual',legend=True)ses_forecast_1.plot(color=COLORS[1], legend=True,label=r'$\alpha=0.2$')ses_1.fittedvalues.plot(color=COLORS[1])ses_forecast_2.plot(color=COLORS[2], legend=True,label=r'$\alpha=0.5$')ses_2.fittedvalues.plot(color=COLORS[2])ses_forecast_3.plot(color=COLORS[3], legend=True,label=r'$\alpha={0:.4f}$'.format(alpha))ses_3.fittedvalues.plot(color=COLORS[3])plt.tight_layout()#plt.savefig('images/ch3_im15.png')plt.show()
執(zhí)行代碼會生成下圖:
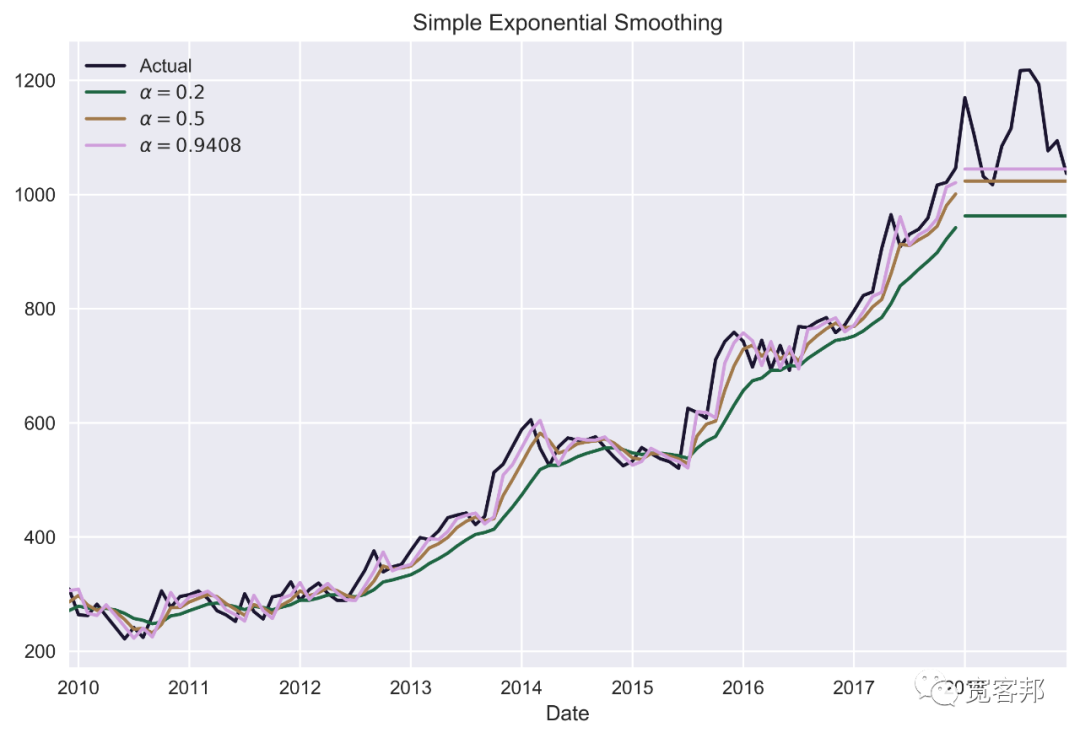
在前面的圖中,我們可以看到我們在本文的介紹中描述的 SES 的特征——預(yù)測是一條平坦的線。我們還可以看到?statsmodels?優(yōu)化程序選擇的最優(yōu)值接近 1。此外,第三個模型的擬合線實際上是觀察到的價格向右移動的線。
8、擬合 Holt 平滑模型的三個變體并創(chuàng)建預(yù)測:
# Holt's model with linear trendhs_1 = Holt(goog_train).fit()hs_forecast_1 = hs_1.forecast(test_length)# Holt's model with exponential trendhs_2 = Holt(goog_train, exponential=True).fit()# equivalent to ExponentialSmoothing(goog_train, trend='mul').fit()hs_forecast_2 = hs_2.forecast(test_length)# Holt's model with exponential trend and dampinghs_3 = Holt(goog_train, exponential=False,damped=True).fit(damping_slope=0.99)hs_forecast_3 = hs_3.forecast(test_length)
9、繪制原始價格和模型的結(jié)果:
goog.plot(color=COLORS[0],title="Holt's Smoothing models",label='Actual',legend=True)hs_1.fittedvalues.plot(color=COLORS[1])hs_forecast_1.plot(color=COLORS[1], legend=True,label='Linear trend')hs_2.fittedvalues.plot(color=COLORS[2])hs_forecast_2.plot(color=COLORS[2], legend=True,label='Exponential trend')hs_3.fittedvalues.plot(color=COLORS[3])hs_forecast_3.plot(color=COLORS[3], legend=True,label='Exponential trend (damped)')plt.tight_layout()#plt.savefig('images/ch3_im16.png')plt.show()

工作原理
在第 2 步到第 5 步中,我們下載了 2010-2018 年 Google 的股票價格,將這些值重新采樣到每月頻率,將數(shù)據(jù)拆分為訓(xùn)練(2010-2017)和測試(2018)集,并繪制了系列圖。
在第 6 步中,我們使用?SimpleExpSmoothing?類及其擬合方法擬合了三個不同的 SES 模型。對于擬合,我們只使用了訓(xùn)練數(shù)據(jù)。我們可以手動選擇平滑參數(shù) (smoothing_level) 的值,但是,最佳實踐是讓?statsmodels?優(yōu)化它以獲得最佳擬合。這種優(yōu)化是通過最小化殘差平方和(誤差)來完成的。我們使用預(yù)測方法創(chuàng)建了預(yù)測,該方法需要我們要預(yù)測的周期數(shù)(等于測試集的長度)。在第 7 步中,我們將結(jié)果可視化并將其與實際股票價格進(jìn)行比較。我們使用擬合模型的擬合值方法提取模型的擬合值。
在第 8 步中,我們使用了?Holt?類(它是更加 通用的ExponentialSmoothing?類)以適合?Holt?的線性趨勢模型。默認(rèn)情況下,模型中的趨勢是線性的,但我們可以通過指定exponential=True?并使用damped=True添加阻尼來使其呈指數(shù)增長。與 SES 的情況一樣,使用不帶參數(shù)的?fit?方法會導(dǎo)致運(yùn)行優(yōu)化例程以確定參數(shù)的最佳值。我們可以通過運(yùn)行fitted_model.params來訪問它。在示例中,我們手動將阻尼參數(shù)的值指定為 0.99,因為優(yōu)化器選擇 1 作為最佳值,這在圖上是無法區(qū)分的。在第 9 步中,我們將結(jié)果可視化。
三次指數(shù)平滑法(holt-winters)
Holt 的方法有一個擴(kuò)展,稱為 Holt-Winter 季節(jié)性平滑法。它考慮了時間序列中的季節(jié)性。此模型沒有單獨的類,但我們可以通過添加seasonal?和seasonal_periods?參數(shù)來調(diào)整ExponentialSmoothing?類。
無需過多贅述,此方法最適合具有趨勢和季節(jié)性的數(shù)據(jù)。該模型有兩種變體,它們具有加法或乘法季節(jié)性。在前一種中,季節(jié)變化在整個時間序列中或多或少是恒定的。在后者中,變化與時間的流逝成比例地變化。
我們首先擬合模型:
SEASONAL_PERIODS = 12# Holt-Winter's model with exponential trendhw_1 = ExponentialSmoothing(goog_train,trend='mul',seasonal='add',seasonal_periods=SEASONAL_PERIODS).fit()hw_forecast_1 = hw_1.forecast(test_length)# Holt-Winter's model with exponential trend and dampinghw_2 = ExponentialSmoothing(goog_train,trend='mul',seasonal='add',seasonal_periods=SEASONAL_PERIODS,damped=True).fit()hw_forecast_2 = hw_2.forecast(test_length)
然后我們繪制結(jié)果:
goog.plot(color=COLORS[0],title="Holt-Winter's Seasonal Smoothing",label='Actual',legend=True)hw_1.fittedvalues.plot(color=COLORS[1])hw_forecast_1.plot(color=COLORS[1], legend=True,label='Seasonal Smoothing')phi = hw_2.model.params['damping_slope']plot_label = f'Seasonal Smoothing (damped with $\phi={phi:.4f}$)'hw_2.fittedvalues.plot(color=COLORS[2])hw_forecast_2.plot(color=COLORS[2], legend=True,label=plot_label)plt.tight_layout()#plt.savefig('images/ch3_im17.png')plt.show()
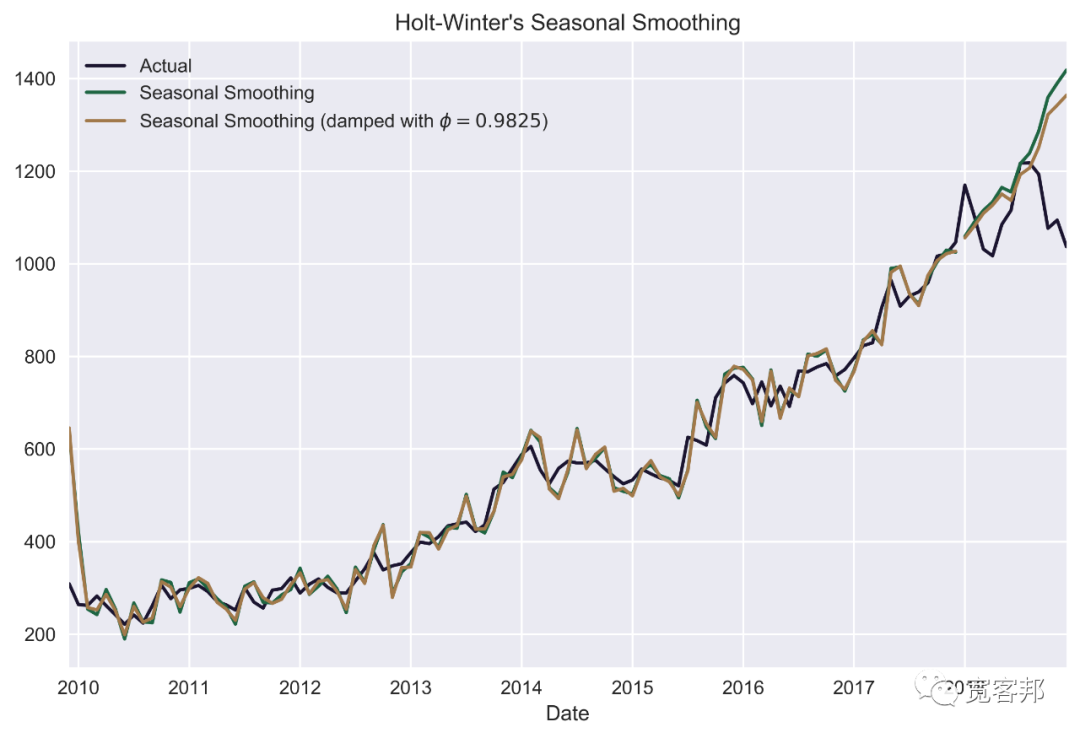
從繪制的預(yù)測圖中,我們可以看到,與 SES 和 Holt 的線性趨勢模型相比,該模型更加靈活。序列開始時的極端擬合值是由于沒有足夠的觀察值可供回溯(我們在處理月度數(shù)據(jù)時選擇了seasonal_periods=12)。

E?N?D

掃描本文最下方二維碼獲取全部完整源碼和Jupyter Notebook 文件打包下載。
↓↓長按掃碼獲取完整源碼↓↓
