一文帶你入門深度學習

點擊上方“Jack Cui”，選擇“設(shè)為星標”

一、前言

大家好，我是?Jack。

承諾的圖解?AI 算法系列教程，今天它來了！

最近，寫了很多 AI 趣味性算法教程，目前寫了 14 篇，其中反響不錯的教程有：

???你的紅色高跟鞋，AI 換臉技術(shù)初體驗???讓圖片動起來，特朗普和蒙娜麗莎深情合唱???為藝術(shù)而生的驚艷算法???百年老照片修復算法，那些高顏值的父母！???「完美復刻」的人物肖像畫生成

但僅限于開心地跑包，這最多只能算是「調(diào)包俠」。

既然來了興致，何不趁熱打鐵，多學些基礎(chǔ)知識，爭取早日邁入「調(diào)參俠」的行列。

大家一起煉丹，一起修煉。

圖解 AI 算法系列教程，不僅僅是涉及深度學習基礎(chǔ)知識，還會有強化學習、遷移學習等，再往小了講就比如拆解目標檢測算法，對抗神經(jīng)網(wǎng)絡（GAN）等等。

如果你喜歡這個 AI 算法系列教程，一定要讓我知道，轉(zhuǎn)發(fā)在看支持，更文更有動力！

難度會逐漸增加，今天咱先熱熱身，來點輕松的，當作這個系列的開篇。

二、深度學習

深度學習（Deep Learning）是近年來發(fā)展十分迅速的研究領(lǐng)域，并且在人 工智能的很多子領(lǐng)域都取得了巨大的成功。從根源來講，深度學習是機器學習的一個分支。

深度學習就是從有限樣例中通過算法總結(jié)出一般性的規(guī)律，并可以應用到新的未知數(shù)據(jù)上。

比如，我們可以從一些歷史病例的集合中總結(jié)出癥狀和疾病之間的規(guī)律。這樣，當有新的病人時，我們可以利用總結(jié)出來的規(guī)律來判斷這個病人得了什么疾病。

那想學深度學習，要掌握哪些基礎(chǔ)知識？直接上圖：

整理了小半天的思維導圖，建議收藏！

深度學習主要由上圖所示的幾個部分組成，想學一個深度學習算法的原理，就看它是什么樣的網(wǎng)絡結(jié)構(gòu)，Loss 是怎么計算的，預處理和后處理都是怎么做的。

權(quán)重初始化和學習率調(diào)整策略、優(yōu)化算法、深度學習框架就那么多，并且也不是所有都要掌握，比如深度學習框架，Pytorch 玩的溜，就能應付大多數(shù)場景。

先有個整體的認知，然后再按照這個思維導圖，逐個知識點學習，最后整合到一起，你會發(fā)現(xiàn)，你也可以自己實現(xiàn)各種功能的算法了。

深度學習的主要目的是從數(shù)據(jù)中自動學習到有效的特征表示，它是怎么工作的？那得從神經(jīng)元說起。

隨著神經(jīng)科學、認知科學的發(fā)展，我們逐漸知道人類的智能行為都和大腦活動有關(guān)。

人腦神經(jīng)系統(tǒng)^[1]是一個非常復雜的組織，包含近 860 億個神經(jīng)元，這 860 億的神經(jīng)元構(gòu)成了超級龐大的神經(jīng)網(wǎng)絡。

我們知道，一個人的智力不完全由遺傳決定，大部分來自于生活經(jīng)驗。也就是說人腦神經(jīng)網(wǎng)絡是一個具有學習能力的系統(tǒng)。

不同神經(jīng)元之間的突觸有強有弱，其強度是可以通過學習（訓練）來不斷改變的，具有一定的可塑性，不同的連接又形成了不同的記憶印痕。

而深度學習的神經(jīng)網(wǎng)絡，就是受人腦神經(jīng)網(wǎng)絡啟發(fā)，設(shè)計的一種計算模型，它從結(jié)構(gòu)、實現(xiàn)機理和功能上模擬人腦神經(jīng)網(wǎng)絡。

比如下圖就是一個最簡單的前饋神經(jīng)網(wǎng)絡，第 0 層稱為輸入層，最后一層稱為輸出層，其他中間層稱為隱藏層。

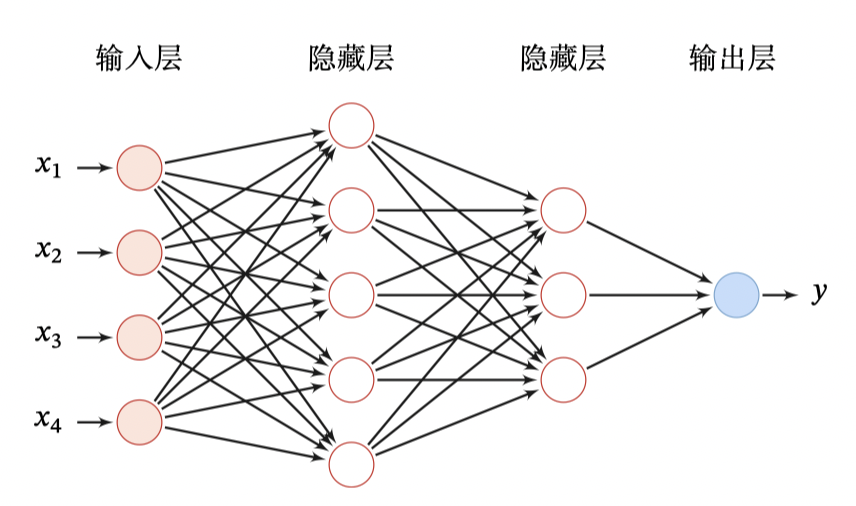
那神經(jīng)網(wǎng)絡如何工作的？網(wǎng)絡層次結(jié)構(gòu)、損失函數(shù)、優(yōu)化算法、權(quán)重初始化、學習率調(diào)整都是如何運作的？

反向傳播給你答案。前方，高能預警！

三、反向傳播

要想弄懂深度學習原理，必須搞定反向傳播^[2]和鏈式求導法則。

先說思維導圖里的網(wǎng)絡層級結(jié)構(gòu)，一個神經(jīng)網(wǎng)絡，可復雜可簡單，為了方便推導，假設(shè)，你有這樣一個網(wǎng)絡層：

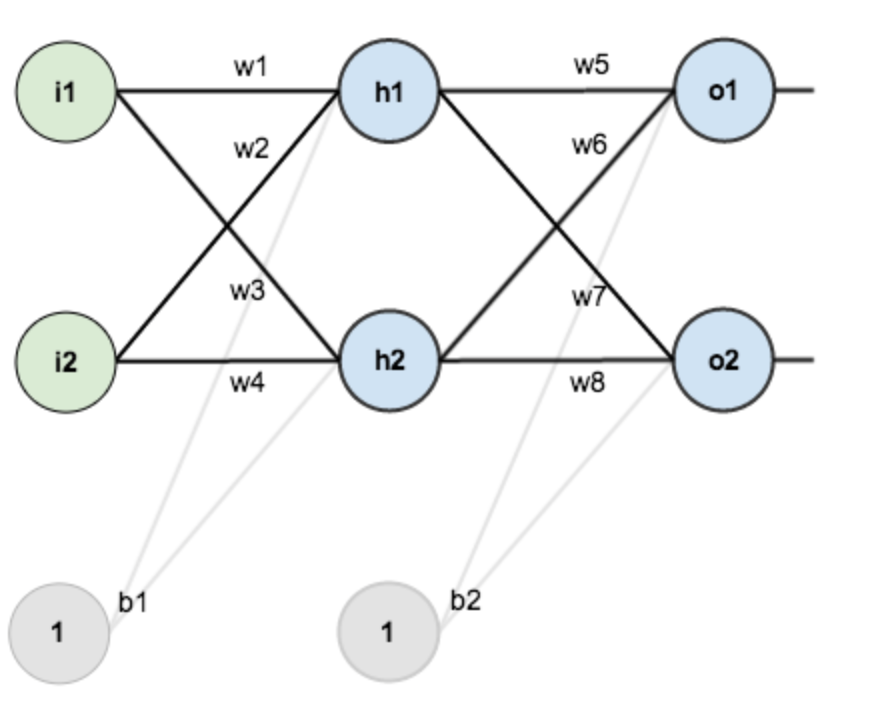
第一層是輸入層，包含兩個神經(jīng)元 i1, i2 和截距項 b1（偏置）；

第二層是隱含層，包含兩個神經(jīng)元 h1, h2 和截距項 b2 ；

第三層是輸出層 o1 和 o2 ，每條線上標的 wi 是層與層之間連接的權(quán)重，激活函數(shù)我們默認為 sigmoid 函數(shù)。

在訓練這個網(wǎng)絡之前，需要初始化這些 wi 權(quán)重，這就是權(quán)重初始化，這里就有不少的初始化方法，我們選擇最簡單的，隨機初始化。

隨機初始化的結(jié)果，如下圖所示：

其中，輸入數(shù)據(jù):?i1=0.05, i2=0.10;

輸出數(shù)據(jù)（期望的輸出） : o1=0.01, o2=0.99;

初始權(quán)重: w1=0.15, w2=0.20, w3=0.25, w4=0.30, w5=0.40, w6=0.45, w7=0.50, w8=0.55。

目標：給出輸入數(shù)據(jù) i1, i2(0.05 和 0.10)，使輸出盡可能與原始輸出o1, o2(0.01 和 0.99)接近。

神經(jīng)網(wǎng)絡的工作流程分為兩步：前向傳播和反向傳播。

1、前向傳播

前向傳播是將輸入數(shù)據(jù)根據(jù)權(quán)重，計算到輸出層。

1）輸入層->隱藏層

計算神經(jīng)元 h1 的輸入加權(quán)和：

神經(jīng)元后面，要跟個激活層，從而引入非線性因素，這就像人的神經(jīng)元一樣，讓細胞處于興奮或抑制的狀態(tài)。

數(shù)學模擬的形式就是通過激活函數(shù)，大于閾值就激活，反之抑制。

常用的激活函如思維導圖所示，這里以非常簡單的 sigmoid 激活函數(shù)為例，它的函數(shù)形式如下：

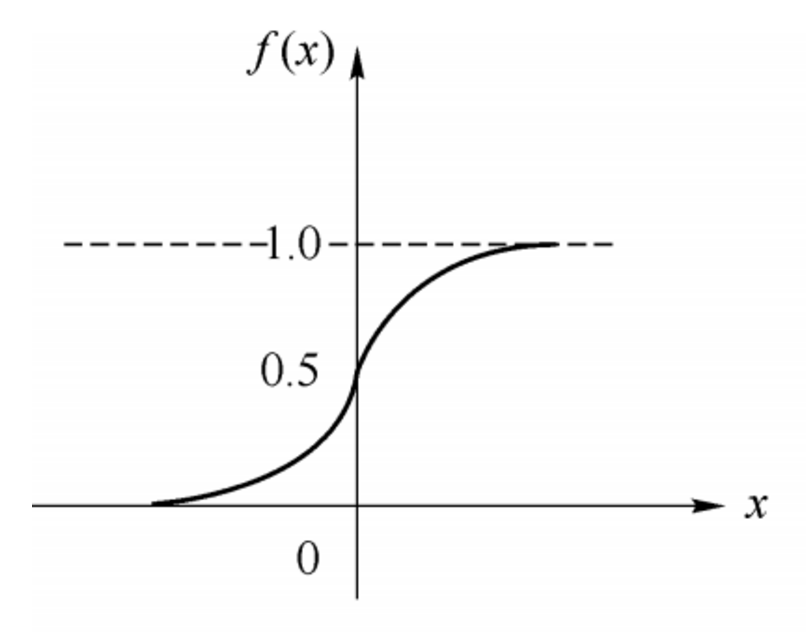
數(shù)學公式：

使用 sigmoid 激活函數(shù)，繼續(xù)計算，神經(jīng)元 h1 的輸出 o_h1：

同理，可計算出神經(jīng)元 h2 的輸出 o_h2：

2）隱藏層->輸出層

計算輸出層神經(jīng)元 o1 和 o2 的值：

這樣前向傳播的過程就結(jié)束了，根據(jù)輸入值和權(quán)重，我們得到輸出值為[0.75136079, 0.772928465]，與實際值（目標）[0.01, 0.99]相差還很遠，現(xiàn)在我們對誤差進行反向傳播，更新權(quán)值，重新計算輸出。

2、反向傳播

前向傳播之后，發(fā)現(xiàn)輸出結(jié)果與期望相差甚遠，這時候就要更新權(quán)重了。

所謂深度學習的訓練（煉丹），學的就是這些權(quán)重，我們期望的是調(diào)整這些權(quán)重，讓輸出結(jié)果符合我們的期望。

而更新權(quán)重的方式，依靠的就是反向傳播。

1）計算總誤差

一次前向傳播過后，輸出值（預測值）與目標值（標簽值）有差距，那得衡量一下有多大差距。

衡量的方法，就是用思維導圖中的損失函數(shù)。

損失函數(shù)也有很多，咱們還是選擇一個最簡單的，均方誤差（MSE loss）。

均方誤差的函數(shù)公式：

根據(jù)公式，直接計算預測值與標簽值的總誤差：

有兩個輸出，所以分別計算 o1 和 o2 的誤差，總誤差為兩者之和：

2）隱含層->輸出層的權(quán)值更新

以權(quán)重參數(shù) w5 為例，如果我們想知道 w5 對整體誤差產(chǎn)生了多少影響，可以用整體誤差對 w5 求偏導求出。

這是鏈式法則，它是微積分中復合函數(shù)的求導法則，就是這個：

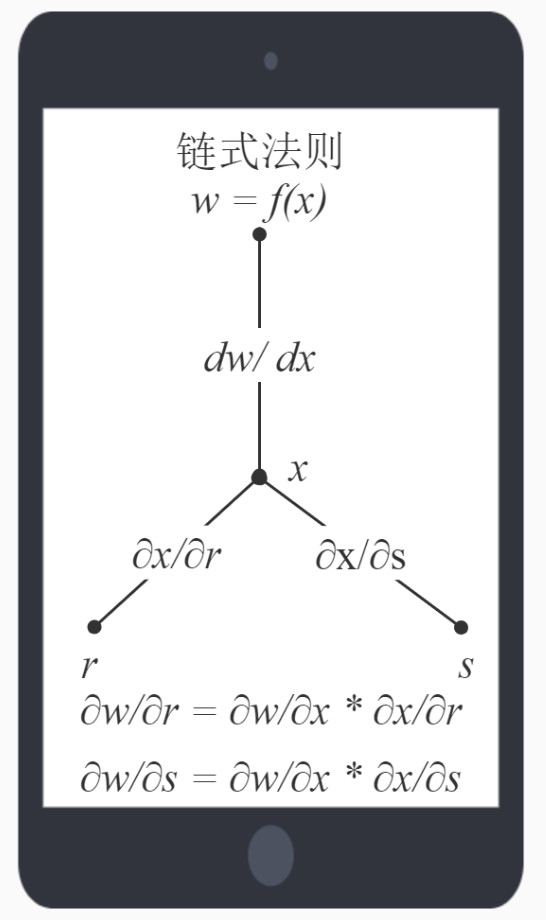
根據(jù)鏈式法則易得：

下面的圖可以更直觀的看清楚誤差是怎樣反向傳播的：

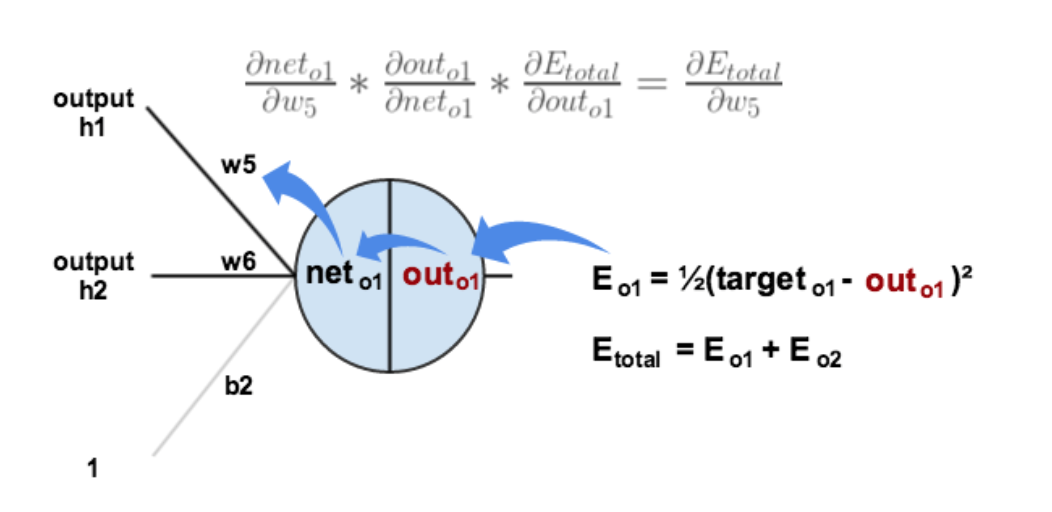
現(xiàn)在我們來分別計算每個式子的值：

計算

計算:

這一步實際上就是對sigmoid函數(shù)求導，比較簡單，可以自己推導一下。

計算：

最后三者相乘：

這樣我們就計算出整體誤差E(total)對 w5 的偏導值。

回過頭來再看看上面的公式，我們發(fā)現(xiàn)：

為了表達方便，用來表示輸出層的誤差：

因此，整體誤差E(total)對w5的偏導公式可以寫成：

如果輸出層誤差計為負的話，也可以寫成：

最后我們來更新 w5 的值：

這個更新權(quán)重的策略，就是思維導圖中的優(yōu)化算法， 是學習率，我們這里取0.5。

如果學習率要根據(jù)迭代的次數(shù)調(diào)整，那就用到了思維導圖中的學習率調(diào)整。

同理，可更新w6,w7,w8:

3）隱含層->隱含層的權(quán)值更新

方法其實與上面說的差不多，但是有個地方需要變一下，在上文計算總誤差對 w5 的偏導時，是從out(o1)->net(o1)->w5，但是在隱含層之間的權(quán)值更新時，是out(h1)->net(h1)->w1,而 out(h1) 會接受 E(o1) 和 E(o2) 兩個地方傳來的誤差，所以這個地方兩個都要計算。

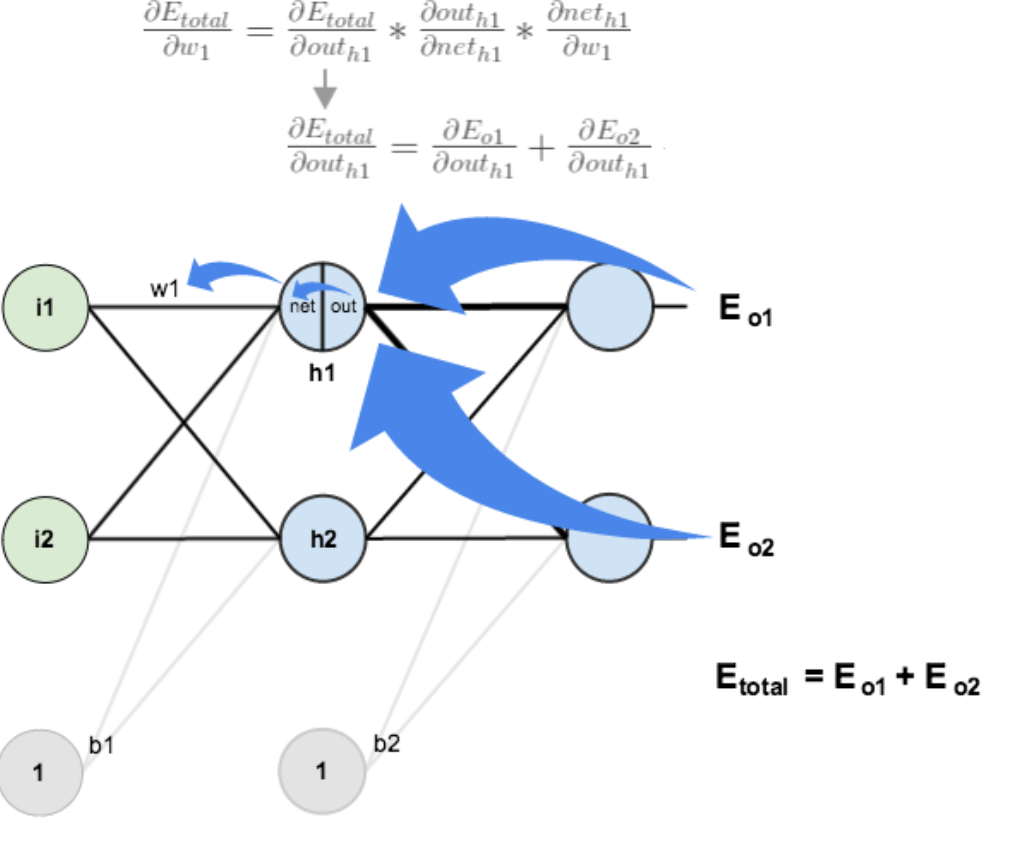
計算：

先計算:

同理，計算出：

兩者相加得到總值：

再計算:

再計算:

最后，三者相乘：

為了簡化公式，用 sigma(h1) 表示隱含層單元 h1 的誤差：

最后，更新 w1 的權(quán)值：

同理，額可更新w2,w3,w4的權(quán)值：

這樣誤差反向傳播法就完成了，最后我們再把更新的權(quán)值重新計算，不停地迭代。

在這個例子中第一次迭代之后，總誤差E(total)由0.298371109下降至0.291027924。

迭代10000次后，總誤差為0.000035085，輸出為[0.015912196,0.984065734]（原輸入為[0.01,0.99]），證明效果還是不錯的。

這就是整個神經(jīng)網(wǎng)絡的工作原理，如果你跟著思路，順利看到這里。那么恭喜你，深度學習的學習算是通過了一關(guān)。

四、Python 實現(xiàn)

整個過程，可以用 Python 代碼實現(xiàn)。

#coding:utf-8
import?random
import?math

#
#???參數(shù)解釋：
#???"pd_"?：偏導的前綴
#???"d_"?：導數(shù)的前綴
#???"w_ho"?：隱含層到輸出層的權(quán)重系數(shù)索引
#???"w_ih"?：輸入層到隱含層的權(quán)重系數(shù)的索引

class?NeuralNetwork:
????LEARNING_RATE?=?0.5

????def?__init__(self,?num_inputs,?num_hidden,?num_outputs,?hidden_layer_weights?=?None,?hidden_layer_bias?=?None,?output_layer_weights?=?None,?output_layer_bias?=?None):
????????self.num_inputs?=?num_inputs

????????self.hidden_layer?=?NeuronLayer(num_hidden,?hidden_layer_bias)
????????self.output_layer?=?NeuronLayer(num_outputs,?output_layer_bias)
????????self.init_weights_from_inputs_to_hidden_layer_neurons(hidden_layer_weights)
????????self.init_weights_from_hidden_layer_neurons_to_output_layer_neurons(output_layer_weights)

????def?init_weights_from_inputs_to_hidden_layer_neurons(self,?hidden_layer_weights):
????????weight_num?=?0
????????for?h?in?range(len(self.hidden_layer.neurons)):
????????????for?i?in?range(self.num_inputs):
????????????????if?not?hidden_layer_weights:
????????????????????self.hidden_layer.neurons[h].weights.append(random.random())
????????????????else:
????????????????????self.hidden_layer.neurons[h].weights.append(hidden_layer_weights[weight_num])
????????????????weight_num?+=?1

????def?init_weights_from_hidden_layer_neurons_to_output_layer_neurons(self,?output_layer_weights):
????????weight_num?=?0
????????for?o?in?range(len(self.output_layer.neurons)):
????????????for?h?in?range(len(self.hidden_layer.neurons)):
????????????????if?not?output_layer_weights:
????????????????????self.output_layer.neurons[o].weights.append(random.random())
????????????????else:
????????????????????self.output_layer.neurons[o].weights.append(output_layer_weights[weight_num])
????????????????weight_num?+=?1

????def?inspect(self):
????????print('------')
????????print('*?Inputs:?{}'.format(self.num_inputs))
????????print('------')
????????print('Hidden?Layer')
????????self.hidden_layer.inspect()
????????print('------')
????????print('*?Output?Layer')
????????self.output_layer.inspect()
????????print('------')

????def?feed_forward(self,?inputs):
????????hidden_layer_outputs?=?self.hidden_layer.feed_forward(inputs)
????????return?self.output_layer.feed_forward(hidden_layer_outputs)

????def?train(self,?training_inputs,?training_outputs):
????????self.feed_forward(training_inputs)

????????#?1.?輸出神經(jīng)元的值
????????pd_errors_wrt_output_neuron_total_net_input?=?[0]?*?len(self.output_layer.neurons)
????????for?o?in?range(len(self.output_layer.neurons)):

????????????#??E/?z?
????????????pd_errors_wrt_output_neuron_total_net_input[o]?=?self.output_layer.neurons[o].calculate_pd_error_wrt_total_net_input(training_outputs[o])

????????#?2.?隱含層神經(jīng)元的值
????????pd_errors_wrt_hidden_neuron_total_net_input?=?[0]?*?len(self.hidden_layer.neurons)
????????for?h?in?range(len(self.hidden_layer.neurons)):

????????????#?dE/dy??=?Σ??E/?z??*??z/?y??=?Σ??E/?z??*?w??
????????????d_error_wrt_hidden_neuron_output?=?0
????????????for?o?in?range(len(self.output_layer.neurons)):
????????????????d_error_wrt_hidden_neuron_output?+=?pd_errors_wrt_output_neuron_total_net_input[o]?*?self.output_layer.neurons[o].weights[h]

????????????#??E/?z??=?dE/dy??*??z?/?
????????????pd_errors_wrt_hidden_neuron_total_net_input[h]?=?d_error_wrt_hidden_neuron_output?*?self.hidden_layer.neurons[h].calculate_pd_total_net_input_wrt_input()

????????#?3.?更新輸出層權(quán)重系數(shù)
????????for?o?in?range(len(self.output_layer.neurons)):
????????????for?w_ho?in?range(len(self.output_layer.neurons[o].weights)):

????????????????#??E?/?w???=??E/?z??*??z?/?w??
????????????????pd_error_wrt_weight?=?pd_errors_wrt_output_neuron_total_net_input[o]?*?self.output_layer.neurons[o].calculate_pd_total_net_input_wrt_weight(w_ho)

????????????????#?Δw?=?α?*??E?/?w?
????????????????self.output_layer.neurons[o].weights[w_ho]?-=?self.LEARNING_RATE?*?pd_error_wrt_weight

????????#?4.?更新隱含層的權(quán)重系數(shù)
????????for?h?in?range(len(self.hidden_layer.neurons)):
????????????for?w_ih?in?range(len(self.hidden_layer.neurons[h].weights)):

????????????????#??E?/?w??=??E/?z??*??z?/?w?
????????????????pd_error_wrt_weight?=?pd_errors_wrt_hidden_neuron_total_net_input[h]?*?self.hidden_layer.neurons[h].calculate_pd_total_net_input_wrt_weight(w_ih)

????????????????#?Δw?=?α?*??E?/?w?
????????????????self.hidden_layer.neurons[h].weights[w_ih]?-=?self.LEARNING_RATE?*?pd_error_wrt_weight

????def?calculate_total_error(self,?training_sets):
????????total_error?=?0
????????for?t?in?range(len(training_sets)):
????????????training_inputs,?training_outputs?=?training_sets[t]
????????????self.feed_forward(training_inputs)
????????????for?o?in?range(len(training_outputs)):
????????????????total_error?+=?self.output_layer.neurons[o].calculate_error(training_outputs[o])
????????return?total_error

class?NeuronLayer:
????def?__init__(self,?num_neurons,?bias):

????????#?同一層的神經(jīng)元共享一個截距項b
????????self.bias?=?bias?if?bias?else?random.random()

????????self.neurons?=?[]
????????for?i?in?range(num_neurons):
????????????self.neurons.append(Neuron(self.bias))

????def?inspect(self):
????????print('Neurons:',?len(self.neurons))
????????for?n?in?range(len(self.neurons)):
????????????print('?Neuron',?n)
????????????for?w?in?range(len(self.neurons[n].weights)):
????????????????print('??Weight:',?self.neurons[n].weights[w])
????????????print('??Bias:',?self.bias)

????def?feed_forward(self,?inputs):
????????outputs?=?[]
????????for?neuron?in?self.neurons:
????????????outputs.append(neuron.calculate_output(inputs))
????????return?outputs

????def?get_outputs(self):
????????outputs?=?[]
????????for?neuron?in?self.neurons:
????????????outputs.append(neuron.output)
????????return?outputs

class?Neuron:
????def?__init__(self,?bias):
????????self.bias?=?bias
????????self.weights?=?[]

????def?calculate_output(self,?inputs):
????????self.inputs?=?inputs
????????self.output?=?self.squash(self.calculate_total_net_input())
????????return?self.output

????def?calculate_total_net_input(self):
????????total?=?0
????????for?i?in?range(len(self.inputs)):
????????????total?+=?self.inputs[i]?*?self.weights[i]
????????return?total?+?self.bias

????#?激活函數(shù)sigmoid
????def?squash(self,?total_net_input):
????????return?1?/?(1?+?math.exp(-total_net_input))

????def?calculate_pd_error_wrt_total_net_input(self,?target_output):
????????return?self.calculate_pd_error_wrt_output(target_output)?*?self.calculate_pd_total_net_input_wrt_input();

????#?每一個神經(jīng)元的誤差是由平方差公式計算的
????def?calculate_error(self,?target_output):
????????return?0.5?*?(target_output?-?self.output)?**?2

????def?calculate_pd_error_wrt_output(self,?target_output):
????????return?-(target_output?-?self.output)

????def?calculate_pd_total_net_input_wrt_input(self):
????????return?self.output?*?(1?-?self.output)

????def?calculate_pd_total_net_input_wrt_weight(self,?index):
????????return?self.inputs[index]


#?文中的例子:

nn?=?NeuralNetwork(2,?2,?2,?hidden_layer_weights=[0.15,?0.2,?0.25,?0.3],?hidden_layer_bias=0.35,?output_layer_weights=[0.4,?0.45,?0.5,?0.55],?output_layer_bias=0.6)
for?i?in?range(10000):
????nn.train([0.05,?0.1],?[0.01,?0.09])
????print(i,?round(nn.calculate_total_error([[[0.05,?0.1],?[0.01,?0.09]]]),?9))


#另外一個例子，可以把上面的例子注釋掉再運行一下:

#?training_sets?=?[
#?????[[0,?0],?[0]],
#?????[[0,?1],?[1]],
#?????[[1,?0],?[1]],
#?????[[1,?1],?[0]]
#?]

#?nn?=?NeuralNetwork(len(training_sets[0][0]),?5,?len(training_sets[0][1]))
#?for?i?in?range(10000):
#?????training_inputs,?training_outputs?=?random.choice(training_sets)
#?????nn.train(training_inputs,?training_outputs)
#?????print(i,?nn.calculate_total_error(training_sets))

五、其他

預處理和后處理就相對簡單很多，預處理就是一些常規(guī)的圖像變換操作，數(shù)據(jù)增強方法等。

后處理每個任務都略有不同，比如目標檢測的非極大值抑制等，這些內(nèi)容可以放在以后再講。

至于深度學習框架的學習，那就是另外一大塊內(nèi)容了，深度學習框架是一種為了深度學習開發(fā)而生的工具，庫和預訓練模型等資源的總和。

我們可以用 Python 實現(xiàn)簡單的神經(jīng)網(wǎng)絡，但是復雜的神經(jīng)網(wǎng)絡，還得靠框架，框架的使用可以大幅度降低我們的開發(fā)成本。

至于學哪種框架，看個人喜好，Pytorch 和 Tensorflow 都行。人生苦短，我選 Pytorch。

六、學習資料推薦

學完本文，只能算是深度學習入門，還有非常多的內(nèi)容需要深入學習。

推薦一些資料，方便感興趣的讀者繼續(xù)研究。

視頻：

• 吳恩達的深度學習公開課^[3]：https://mooc.study.163.com/university/deeplearning_ai

書籍：

• 《神經(jīng)網(wǎng)絡與深度學習》
• 《PyTorch深度學習實戰(zhàn)》

開源項目：

• Pytorch教程 1：https://github.com/yunjey/pytorch-tutorial
• Pytorch教程 2：https://github.com/pytorch/tutorials

七、絮叨

學習的積累是個漫長而又孤獨的過程，厚積才能薄發(fā)，有不懂的知識就多看多想，要相信最后勝利的，是堅持下去的那個人。

本文硬核，如果喜歡，還望轉(zhuǎn)發(fā)、再看多多支持。

我是 Jack，我們下期見。

參考資料