【寫在前面】

無論是自己實現一個神經網絡，還是使用一個內置的庫來學習神經網絡，了解 Sigmoid函數的意義是至關重要的。Sigmoid函數是理解神經網絡如何學習復雜問題的關鍵 。這個函數也是學習其他函數的基礎，這些函數可以為深度學習架構中的監(jiān)督學習提供高效的解決方案。本文分為三個部分：

1、Sigmoid函數

2、線性與非線性可分性

3、為什么神經網絡可以通過使用Sigmoid函數，作出復雜的決策邊界

1. Sigmoid Function

1.1. ?Sigmoid函數的性質和恒等式

Sigmoid函數是 Logistic函數的一種特殊形式，通常用 σ (x)或 sig (x)來表示。如下所示：

Sigmoid 函數是一條 s 形曲線，如下圖中的綠線所示。該圖還顯示了粉紅色的導數圖形：

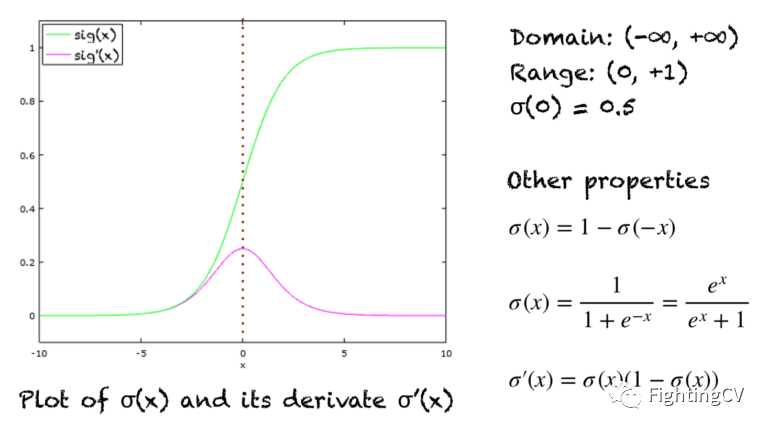
1.2. ?Sigmoid——壓縮函數

Sigmoid函數也可以作為壓縮函數，因為它的域是所有實數的集合，它的范圍是(0,1)。因此，如果函數的輸入是一個非常大的負數或非常大的正數，則輸出總是介于0和1之間。在-∞和 + ∞之間的任何數字也是如此。

1.3. ?Sigmoid——激活函數

Sigmoid函數被用作神經網絡中的激活函數。為了回顧什么是激活函數神經元，下面的圖顯示了激活函數神經元在神經網絡的一個層中所起的作用。輸入的加權和通過一個激活函數，這個輸出作為下一層的輸入。

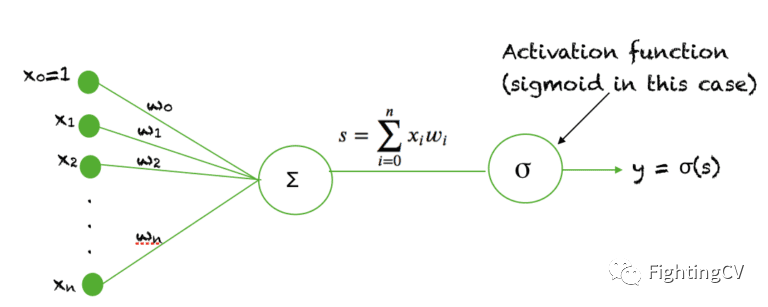
當一個神經元的激活函數是一個 Sigmoid函數時，這個單元的輸出保證總是介于0和1之間。此外，由于 Sigmoid是一個非線性函數，這個單元的輸出將是一個非線性函數的加權和的輸入。這種以Sigmoid函數為激活函數的神經元被稱為sigmoid unit 。

2. 線性與非線性可分性?

假設我們有一個典型的分類問題，我們在空間中有一組點，每個點被分配一個類標簽。如果一條直線(或 n 維空間中的一個超平面)可以將這兩類分開，那么我們就有一個線性可分問題。另一方面，如果一條直線不足以劃分這兩類，那么我們就有一個非線性可分問題。下圖顯示了二維空間中的數據。每個點被分配一個紅色或藍色的類標簽。左圖顯示了一個線性可分問題，該問題需要一個線性邊界來區(qū)分兩類問題。右圖顯示了一個非線性可分問題，需要一個非線性決策邊界。

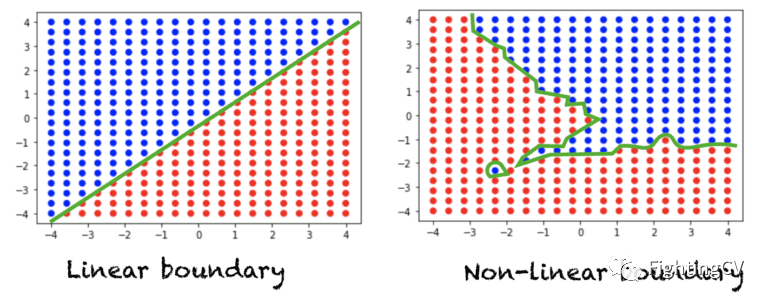
對于三維空間，線性決策邊界可以用平面方程來描述。對于 n 維空間，線性決策邊界由超平面方程描述。

3. 為什么 Sigmoid函數在神經網絡中很重要？

如果我們在神經網絡中使用線性激活函數，那么這個模型只能學習線性可分問題。然而，只要在隱藏層中增加一個隱藏層和一個 Sigmoid激活函數，神經網絡就可以很容易地學習一個非線性可分問題 。使用非線性函數產生非線性邊界，因此，Sigmoid函數可以用于神經網絡學習復雜的決策函數。

在神經網絡中，可以用作激活函數的非線性函數必須是一個單調遞增 的函數。例如，sin (x)或 cos (x)不能用作激活函數。另外，激活函數應該定義為任意處 ，并且在實數空間中任意處都是連續(xù)的 。這個函數還要求在整個實數空間上是可微 的。

通常，反向傳播算法使用梯度下降法學習神經網絡的權重。為了得到這個算法，需要對激活函數進行求導數。而由于Sigmoid函數是單調的，連續(xù)的，到處可微的 ，再加上它的導數可以用它自己來表示 的特性，使得當使用反向傳播算法時，很容易推導出學習神經網絡中的權重的更新方程。