本文將基于不平衡數(shù)據(jù)，使用Python進(jìn)行反欺詐模型數(shù)據(jù)分析實戰(zhàn)，模擬分類預(yù)測模型中因變量分類出現(xiàn)不平衡時該如何解決，具體的案例應(yīng)用場景除反欺詐外，還有客戶違約和疾病檢測等。只要是因變量中各分類占比懸殊，就可對其使用一定的采樣方法，以達(dá)到除模型調(diào)優(yōu)外的精度提升。主要將分為兩個部分：

• 原理介紹
  

• Python實戰(zhàn)
  

原理介紹

與其花大量的時間對建好的模型進(jìn)行各種調(diào)優(yōu)操作，不如在一開始就對源數(shù)據(jù)進(jìn)行系統(tǒng)而嚴(yán)謹(jǐn)?shù)奶幚怼６鴶?shù)據(jù)處理背后的算法原理又常是理解代碼的支撐。所以本節(jié)將詳細(xì)介紹不平衡采樣的多種方法。

在以往的學(xué)習(xí)中，數(shù)據(jù)大多是對稱分布的，就像下圖一樣，即正負(fù)樣本的數(shù)量相當(dāng)。這樣可以更好的把注意力集中在特定的算法上，而不被其他問題干擾。以分離算法為例，它的目標(biāo)是嘗試學(xué)習(xí)出一個能夠分辨二者的分離器（分類器）。根據(jù)不同的數(shù)學(xué)、統(tǒng)計或幾何假設(shè)，達(dá)成這一目標(biāo)的方法很多：邏輯回歸，嶺回歸，決策樹，和各種聚類算法等。

但當(dāng)我們開始面對真實的、未經(jīng)加工過的數(shù)據(jù)時，很快就會發(fā)現(xiàn)這些數(shù)據(jù)要嘈雜且不平衡得多。真實數(shù)據(jù)看起來更像是如下圖般毫無規(guī)律且零散。對于不平衡類的研究通常認(rèn)為 “不平衡” 意味著少數(shù)類只占 10% ~ 20%。但其實這已經(jīng)算好的了，在現(xiàn)實中的許多例子會更加的不平衡（1~2%），如規(guī)劃中的客戶信用卡欺詐率，重大疾病感染率等。就像下圖一樣

如果我們拿到像上圖那樣的數(shù)據(jù)，哪怕經(jīng)過了清洗，已經(jīng)非常整潔了，之后把它們直接丟進(jìn)邏輯回歸或者決策樹和神經(jīng)網(wǎng)絡(luò)模型里面的話，效果一定會見得好嗎？。以根據(jù)患者體征來預(yù)測其得某種罕見病為例：可能模型在預(yù)測該患者不得病上特準(zhǔn)，畢竟不得病的數(shù)據(jù)占到了98%，那把剩下的得病的那 2% 也都預(yù)測成了不得病的情況下模型的整體準(zhǔn)確度還是非常高...但整體準(zhǔn)確度高并不代表模型在現(xiàn)實情況就能有相同的優(yōu)良表現(xiàn)，所以最好還是能夠拿到 1:1 的數(shù)據(jù)，這樣模型預(yù)測出來的結(jié)果才最可靠。

所以對于這類數(shù)據(jù)，常見而有效的處理方式有基本的數(shù)據(jù)處理、調(diào)整樣本權(quán)重與使用模型等三類。

本文將專注于從數(shù)據(jù)處理的角度來解決數(shù)據(jù)不平衡問題，后續(xù)推文會涉及使用模型來處理。

注意事項：

• 評估指標(biāo)：使用精確度（Precise Rate）、召回率（Recall Rate）、Fmeasure或ROC曲線、準(zhǔn)確度召回曲線（precision-recall curve）；不要使用準(zhǔn)確度（Accurate Rate）
• 不要使用模型給出的標(biāo)簽，而是要概率估計；得到概率估計之后，不要盲目地使用0.50的決策閥值來區(qū)分類別，應(yīng)該再檢查表現(xiàn)曲線之后再自己決定使用哪個閾值。

問：為什么數(shù)據(jù)處理的幾種采樣方法都只對訓(xùn)練集進(jìn)行操作？

答：因為原始數(shù)據(jù)集的 0-1 比為 1:99，所以隨即拆分成的訓(xùn)練集和測試集的 0-1 比也差不多是 1:99，又因為我們用訓(xùn)練集來訓(xùn)練模型，如果不對訓(xùn)練集的數(shù)據(jù)做任何操作，得出來模型就會在預(yù)測分類0的準(zhǔn)度上比1高，而我們希望的是兩者都要兼顧，所以我們才要使用欠采樣或者過采樣對訓(xùn)練集進(jìn)行處理，使訓(xùn)練集的 0-1 比在我們之前聊到的 1:1 ~ 1:10 這個比較合適的區(qū)間，用這樣的訓(xùn)練集訓(xùn)練出來的模型的泛化能力會更強(qiáng)。以打靶作為比喻，靶心面積很小，對應(yīng)了占比小的違約客戶群體。在 0-1 比為 1:99 的測試集的嚴(yán)酷考驗下，模型打中靶心（成功預(yù)測違約客戶）與打中靶心周圍（成功預(yù)測履約客戶）的概率都得到了保證。

欠采樣與過采樣

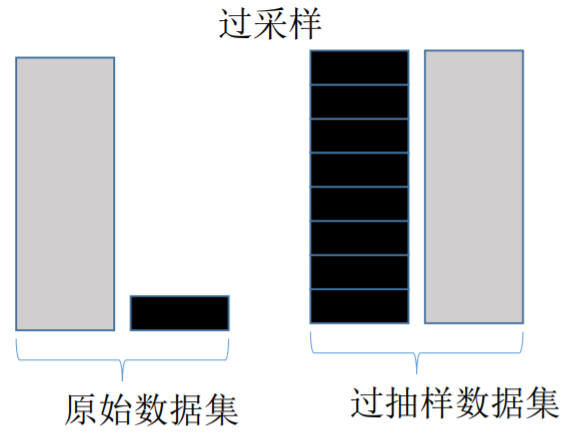
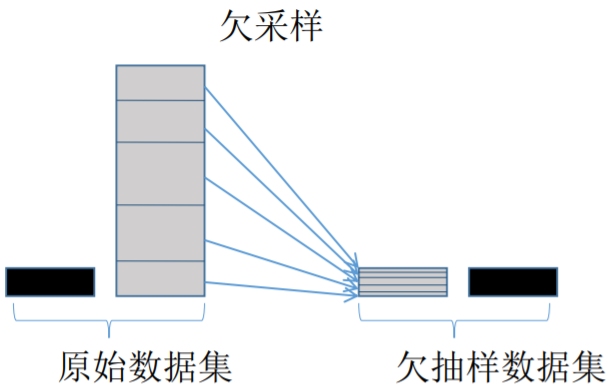
過采樣會隨機(jī)復(fù)制少數(shù)樣例以增大它們的規(guī)模。欠采樣則隨機(jī)地少采樣主要的類。一些數(shù)據(jù)科學(xué)家（天真地）認(rèn)為過采樣更好，因為其會得到更多的數(shù)據(jù)，而欠采樣會將數(shù)據(jù)丟掉。但請記住復(fù)制數(shù)據(jù)不是沒有后果的——因為其會得到復(fù)制出來的數(shù)據(jù)，它就會使變量的方差表面上比實際上更小。而過采樣的好處是它也會復(fù)制誤差的數(shù)量：如果一個分類器在原始的少數(shù)類數(shù)據(jù)集上做出了一個錯誤的負(fù)面錯誤，那么將該數(shù)據(jù)集復(fù)制五次之后，該分類器就會在新的數(shù)據(jù)集上出現(xiàn)六個錯誤。相對地，欠采樣會讓獨立變量（independent variable）的方差看起來比其實際的方差更高。

Tomek Link 法欠采樣

上圖為 Tomek Link 欠采樣法的核心。不難發(fā)現(xiàn)左邊的分布中 0-1 兩個類別之間并沒有明顯的分界。Tomek Link 法處理后，將占比多的一方（0），與離它(0)最近的一個少的另一方 (1) 配對，而后將這個配對刪去，這樣一來便如右邊所示構(gòu)造出了一條明顯一些的分界線。所以說欠采樣需要在占比少的那一類的數(shù)據(jù)量比較大的時候使用（大型互聯(lián)網(wǎng)公司與銀行），畢竟一命抵一命...

Random Over Sampling 隨機(jī)過采樣

隨機(jī)過采樣并不是將原始數(shù)據(jù)集中占比少的類簡單的乘個指定的倍數(shù)，而是對較少類按一定比例進(jìn)行一定次數(shù)的隨機(jī)抽樣，然后將每次隨機(jī)抽樣所得到的數(shù)據(jù)集疊加。但如果只是簡單的隨機(jī)抽樣也難免會出現(xiàn)問題，因為任意兩次的隨機(jī)抽樣中，可能會有重復(fù)被抽到的數(shù)據(jù)，所以經(jīng)過多次隨機(jī)抽樣后疊加在一起的數(shù)據(jù)中可能會有不少的重復(fù)值，這便會使數(shù)據(jù)的變異程度減小。所以這是隨機(jī)過采樣的弊端。

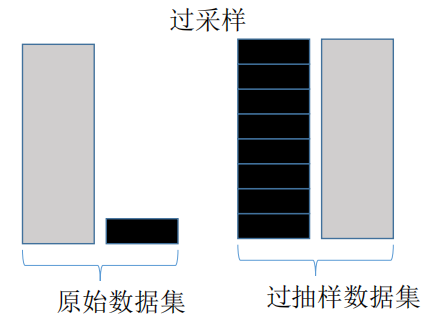
SMOTE 過采樣

SMOTE 過采樣法的出現(xiàn)正好彌補(bǔ)了隨機(jī)過采樣的不足，其核心步驟如下圖但SMOTE 并不是一點壞處都沒有。上圖的數(shù)據(jù)分布 SMOTE 方法的步驟示意圖是比較理想的情況（兩個類別分得還比較開），通常數(shù)據(jù)不平衡的散點圖應(yīng)該是像下面這樣的：而這個時候如果我們依然使用 SMOTE 來過采樣的話就會出現(xiàn)下面的問題理想情況下的圖中我們可以看出黑點的分布似乎是可以用一條線連起來的，而現(xiàn)實情況中的數(shù)據(jù)往往太過分散，比如上圖中的黑點是呈現(xiàn)U型曲線的分布，在這個情況下，SMOTE 算法的第四步作中間插值后，可能這個新插入的點剛好就是某個白點所在的點。本來是 0 的地盤，密密集集的0當(dāng)中突然給生硬的插進(jìn)去了一個1......這就使數(shù)據(jù)又重復(fù)了

綜合采樣

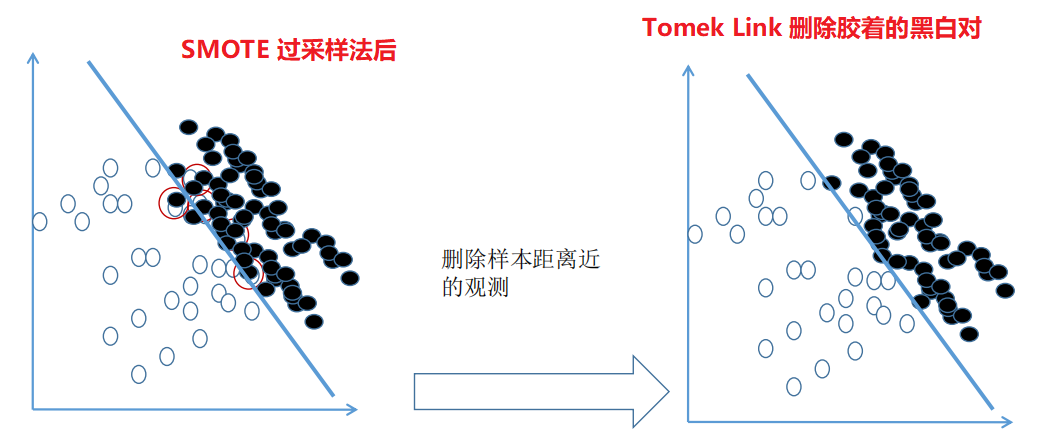
綜合采樣的核心：先使用過采樣，擴(kuò)大樣本后再對處在膠著狀態(tài)的點用 Tomek Link 法進(jìn)行刪除，有時候甚至連 Tomek Link 都不用，直接把離得近的對全部刪除，因為在進(jìn)行過采樣后，0 和 1 的樣本量已經(jīng)達(dá)到了 1：1。

Python實戰(zhàn)

數(shù)據(jù)探索

首先導(dǎo)入相關(guān)包

import?pandas?as?pd
import?numpy?as?np
import?matplotlib.pyplot?as?plt
import?seaborn?as?sns

為了方便敘述建模流程，這里準(zhǔn)備了兩個脫敏數(shù)據(jù)集：一個訓(xùn)練集一個測試集

train?=?pd.read_csv('imb_train.csv')
test?=?pd.read_csv('imb_test.csv')

print(f'訓(xùn)練集數(shù)據(jù)長度：{len(train)}，測試集數(shù)據(jù)長度：{len(test)}')
train.sample(3)

稍微解釋下參數(shù):

• X1 ~ X5：自變量，
• cls：因變量 care life of science - 科學(xué)關(guān)愛生命 0-不得病，1-得病

現(xiàn)在查看測試集與訓(xùn)練集的因變量分類情況

print('訓(xùn)練集中，因變量 cls 分類情況：')
print(train['cls'].agg(['value_counts']).T)
print('='*55?+?'\n')

print('測試集中，因變量 cls 分類情況：')
print(test['cls'].agg(['value_counts']).T)

可知訓(xùn)練集和測試集中的占比少的類別 1 實在是太少了，比較嚴(yán)重的不平衡，我們還可以使用 Counter 庫統(tǒng)計一下兩個數(shù)據(jù)集中因變量的分類情況，不難發(fā)現(xiàn)數(shù)據(jù)不平衡問題還是比較嚴(yán)重

from?collections?import?Counter
print('訓(xùn)練集中因變量 cls 分類情況：{}'.format(Counter(train['cls'])))
print('測試集因變量 cls 分類情況：{}'.format(Counter(test['cls'])))
#訓(xùn)練集中因變量 cls 分類情況：Counter({0: 13644, 1: 356})
#測試集因變量 cls 分類情況：Counter({0: 5848, 1: 152})

不同的抽樣方法對訓(xùn)練集進(jìn)行處理

在處理前再次重申兩點：

• 測試集不做任何處理！保留嚴(yán)峻的比例考驗來測試模型。
• 訓(xùn)練模型時用到的數(shù)據(jù)才是經(jīng)過處理的，0-1 比例在 1：1 ~ 1：10 之間拆分自變量與因變量

拆分自變量與因變量

y_train?=?train['cls'];????????y_test?=?test['cls']
X_train?=?train.loc[:,?:'X5'];??X_test?=?test.loc[:,?:'X5']
X_train.sample(),?y_train[:1]?
#(????????????X1????????X2????????X3???????X4????????X5
#?9382?-1.191287??1.363136?-0.705131?-1.24394?-0.520264,?0????0
#?Name:?cls,?dtype:?int64)

抽樣的幾種方法

• Random Over Sampling：隨機(jī)過抽樣
• SMOTE 方法過抽樣
• SMOTETomek 綜合抽樣

我們將用到imbalance learning這個包，pip install imblearn安裝一下即可，下面是不同抽樣方法的核心代碼，具體如何使用請看注釋

from?imblearn.over_sampling?import?RandomOverSampler
print('不經(jīng)過任何采樣處理的原始 y_train 中的分類情況：{}'.format(Counter(y_train)))

#?采樣策略 sampling_strategy =?'auto'?的 auto 默認(rèn)抽成 1：1，
?##?如果想要另外的比例如杰克所說的 1：5，甚至底線 1:10，需要根據(jù)文檔自行調(diào)整參數(shù)
?##?文檔：https://imbalanced-learn.readthedocs.io/en/stable/generated/imblearn.over_sampling.RandomOverSampler.html
#?先定義好好，未開始正式訓(xùn)練擬合
ros?=?RandomOverSampler(random_state=0,?sampling_strategy='auto')?
X_ros,?y_ros?=?ros.fit_sample(X_train,?y_train)
print('隨機(jī)過采樣后，訓(xùn)練集 y_ros 中的分類情況：{}'.format(Counter(y_ros)))

#?同理，SMOTE?的步驟也是如此
from?imblearn.over_sampling?import?SMOTE
sos?=?SMOTE(random_state=0)
X_sos,?y_sos?=?sos.fit_sample(X_train,?y_train)
print('SMOTE過采樣后，訓(xùn)練集 y_sos 中的分類情況：{}'.format(Counter(y_sos)))

#?同理，綜合采樣（先過采樣再欠采樣）
##?#?combine?表示組合抽樣，所以?SMOTE?與?Tomek?這兩個英文單詞寫在了一起
from?imblearn.combine?import?SMOTETomek
kos?=?SMOTETomek(random_state=0)??#?綜合采樣
X_kos,?y_kos?=?kos.fit_sample(X_train,?y_train)
print('綜合采樣后，訓(xùn)練集 y_kos 中的分類情況：{}'.format(Counter(y_kos)))

不難看出兩種過采樣方法都將原來 y_train 中的占比少的分類 1 提到了與 0 數(shù)量一致的情況，但因為綜合采樣在過采樣后會使用欠采樣，所以數(shù)量會稍微少一點點

決策樹建模

看似高大上的梯度優(yōu)化其實也被業(yè)內(nèi)稱為硬調(diào)優(yōu)，即每個模型參數(shù)都給幾個潛在值，而后讓模型將其自由組合，根據(jù)模型精度結(jié)果記錄并輸出最佳組合，以用于測試集的驗證。首先導(dǎo)入相關(guān)包

from?sklearn.tree?import?DecisionTreeClassifier
from?sklearn?import?metrics
from?sklearn.model_selection?import?GridSearchCV

現(xiàn)在創(chuàng)建決策樹類，但并沒有正式開始訓(xùn)練模型

clf?=?DecisionTreeClassifier(criterion='gini',?random_state=1234)
#?梯度優(yōu)化
param_grid?=?{'max_depth':[3,?4,?5,?6],?'max_leaf_nodes':[4,?6,?8,?10,?12]}
#?cv?表示是創(chuàng)建一個類，還并沒有開始訓(xùn)練模型
cv?=?GridSearchCV(clf,?param_grid=param_grid,?scoring='f1')

如下是模型的訓(xùn)練數(shù)據(jù)的組合,注意！這里的數(shù)據(jù)使用大有玄機(jī),第一組數(shù)據(jù)X，y_train是沒有經(jīng)過任何操作的,第二組ros為隨機(jī)過采樣，第三組sos為SMOTE過采樣，最后一組kos則為綜合采樣

data?=?[[X_train,?y_train],
????????[X_ros,?y_ros],
????????[X_sos,?y_sos],
????????[X_kos,?y_kos]]

現(xiàn)在對四組數(shù)據(jù)分別做模型，要注意其實recall和precision的用處都不大，看auc即可，recall：覆蓋率，預(yù)測出分類為0且正確的，但本來數(shù)據(jù)集中分類為0的占比本來就很大。而且recall是以閾值為 0.5 來計算的，那我們就可以簡單的認(rèn)為預(yù)測的欺詐概率大于0.5就算欺詐了嗎？還是說如果他的潛在欺詐概率只要超過 20% 就已經(jīng)算為欺詐了呢？

for?features,?labels?in?data:
????cv.fit(features,?labels)?#?對四組數(shù)據(jù)分別做模型
????#?注意：X_test 是從來沒被動過的，回應(yīng)了理論知識：
?????##?使用比例優(yōu)良的(1:1~1:10)訓(xùn)練集來訓(xùn)練模型，用殘酷的(分類為1的僅有2%)測試集來考驗?zāi)Ｐ?/span>
????predict_test?=?cv.predict(X_test)?
????print('auc:%.3f'?%metrics.roc_auc_score(y_test,?predict_test),?
??????????'recall:%.3f'?%metrics.recall_score(y_test,?predict_test),
??????????'precision:%.3f'?%metrics.precision_score(y_test,?predict_test))

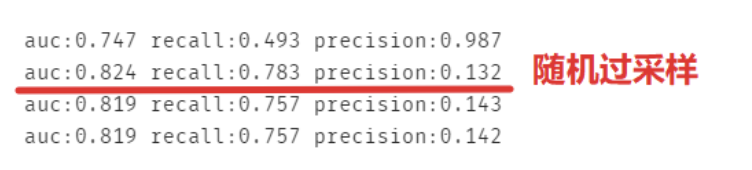可以發(fā)現(xiàn)并不一定是綜合采樣就一定高分，畢竟每份數(shù)據(jù)集都有屬于它自己的特征，不過一點都不處理的模型的 auc 是最低的。

最后總結(jié)一下，隨機(jī)過采樣，SMOTE過采樣與綜合采樣只是解決數(shù)據(jù)不平衡問題方法中的冰山一角，后面還會繼續(xù)深入淺出使用其他模型來平衡數(shù)據(jù)，本文使用的數(shù)據(jù)及源碼可以使用電腦點擊閱讀原文下載。