程序員必備的幾種常見排序算法和搜索算法總結(jié)

前言

最近為了鞏固一下自己的算法基礎(chǔ),又把算法書里的基本算法刷了一遍, 特地總結(jié)一下前端工程師需要了解的排序算法和搜索算法知識,雖然還有很多高深算法需要了解, 但是基礎(chǔ)還是要好好鞏固一下的.本文將以圖文的形式為大家介紹如下算法知識,希望在讀完之后大家能有所收獲:

• 冒泡排序及其優(yōu)化
• 選擇排序
• 插入排序
• 歸并排序
• 快速排序
• 順序搜索
• 二分搜索

正文

我想對于每個前端工程師來說, 最頭疼的就是算法問題, 但是算法往往也是衡量一個人編程能力的一個很重要的指標.目前很多主流框架和庫都應(yīng)用了大量的算法和設(shè)計模式,為了讓自己的段位更高,我們只能不斷的"打怪"(也就是刷算法)升級,才能成為"最強王者".

其實前端發(fā)展這么多年, 越來越偏向于精細化開發(fā), 很多超級應(yīng)用(比如淘寶,微信)都在追求極致的用戶體驗, 時間就是金錢,這要求工程師們不能像以前那樣,開發(fā)的程序只要能用就行, 我們往往還要進行更加細致的測試(包括單元測試, 性能測試等),就拿排序來說, 對于大規(guī)模數(shù)據(jù)量的排序, 我們采用冒泡排序肯定是要被瘋狂吐槽的,因為冒泡排序的性能極差(復(fù)雜度為O(n^2).在真實項目中我們往往不會采用冒泡排序,更多的會用快速排序或者希爾排序.關(guān)于排序算法性能問題我在

• 《前端算法系列》如何讓前端代碼速度提高60倍

有詳細介紹. 接下來就讓我們來一起學(xué)習(xí)如何實現(xiàn)文章開頭的幾個常用排序和搜索算法吧.

1. 冒泡排序及其優(yōu)化

我們在學(xué)排序算法時, 最容易掌握的就是冒泡排序, 因為其實現(xiàn)起來非常簡單,但是從運行性能的角度來看, 它卻是性能最差的一個.

冒泡排序的實現(xiàn)思路是比較任何兩個相鄰的項, 如果前者比后者大, 則將它們互換位置.

為了更方便的展示冒泡排序的過程和性能測試,筆者先寫幾個工具方法,分別為動態(tài)生成指定個數(shù)的隨機數(shù)組,?生成元素位置序列的方法,代碼如下:

// 生成指定個數(shù)的隨機數(shù)組
const generateArr = (num = 10) => {
  let arr = []
  for(let i = 0; i< num; i++) {
    let item = Math.floor(Math.random() * (num + 1))
    arr.push(item)
  }
  return arr
}

// 生成指定個數(shù)的元素x軸坐標
const generateArrPosX = (n= 10, w = 6, m = 6) => {
  let pos = []
  for(let i = 0; i< n; i++) {
    let item = (w + m) * i
    pos.push(item)
  }
  return pos
}

有了以上兩個方法,我們就可以生成任意個數(shù)的數(shù)組以及數(shù)組項坐標了,這兩個方法接下來我們會用到.

我們來直接寫個乞丐版的冒泡排序算法:

bubbleSort(arr = []) {
    let len = arr.length
    for(let i = 0; i< len; i++) {
      for(let j = 0; j < len - 1; j++) {
        if(arr[j] > arr[j+1]) {
          // 置換
          [arr[j], arr[j+1]] = [arr[j+1], arr[j]]
        }
      }
    }
    return arr
  }

接下來我們來測試一下, 我們用generateArr方法生成60個數(shù)組項的數(shù)組, 并動態(tài)生成元素坐標:

// 生成坐標
const pos = generateArrPosX(60)
// 生成60個項的數(shù)組
const arr = generateArr(60)

執(zhí)行代碼后會生成下圖隨機節(jié)點結(jié)構(gòu):

有關(guān)css部分這里就不介紹了,大家可以自己實現(xiàn).接下來我們就可以測試我們上面寫的冒泡排序了,當我們點擊排序時,結(jié)果如下:

可以看到數(shù)組已按照順序排好了,我們可以使用console.time來測量代碼執(zhí)行所用的時間,上面"乞丐版"冒泡排序耗時為0.2890625ms.

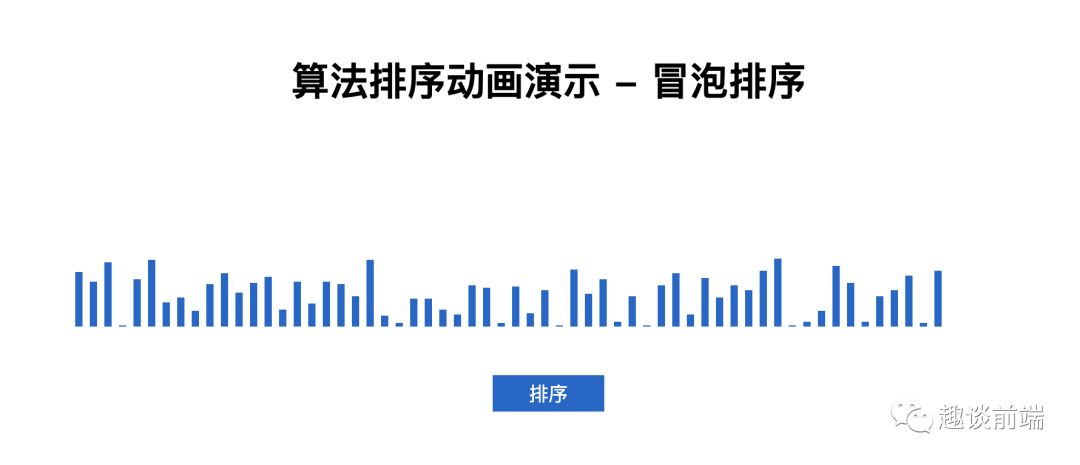
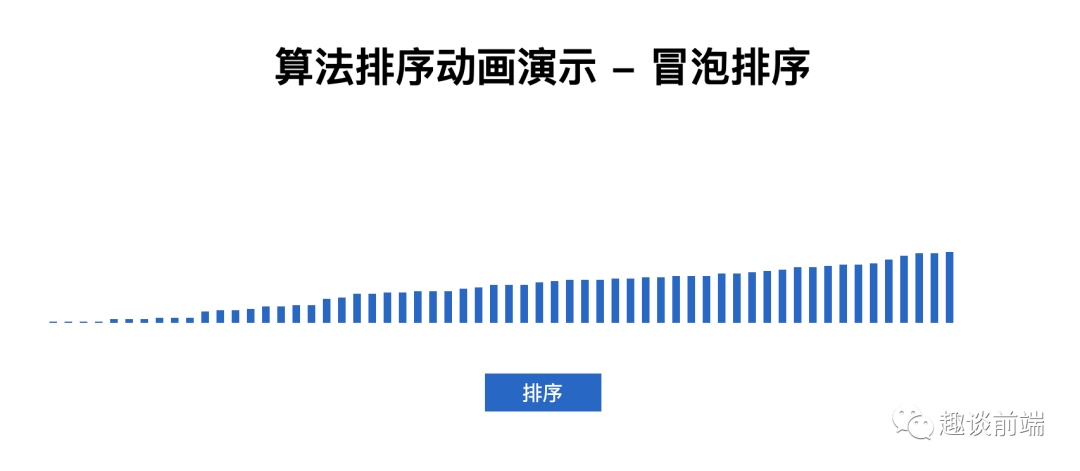
我們深入分析代碼就可以知道兩層for循環(huán)排序?qū)е铝撕芏喽嘤嗟呐判?如果我們從內(nèi)循環(huán)減去外循環(huán)中已跑過的輪數(shù),就可以避免內(nèi)循環(huán)中不必要的比較,所以我們代碼優(yōu)化如下:

// 冒泡排序優(yōu)化版
bubbleSort(arr = []) {
  let len = arr.length
  // 優(yōu)化
  for(let i = 0; i< len; i++) {
    for(let j = 0; j < len - 1 - i; j++) {
      if(arr[j] > arr[j+1]) {
        // 置換
        [arr[j], arr[j+1]] = [arr[j+1], arr[j]]
      }
    }
  }
  return arr
}

經(jīng)過優(yōu)化的冒泡排序耗時:0.279052734375ms, 比之前稍微好了一丟丟, 但仍然不是推薦的排序算法.

2. 選擇排序

選擇排序的思路是找到數(shù)據(jù)結(jié)構(gòu)中的最小值并將其放置在第一位,接著找到第二個最小值并將其放到第二位,依次類推.

我們還是按照之前的模式,生成一個60項的數(shù)組, 如下:

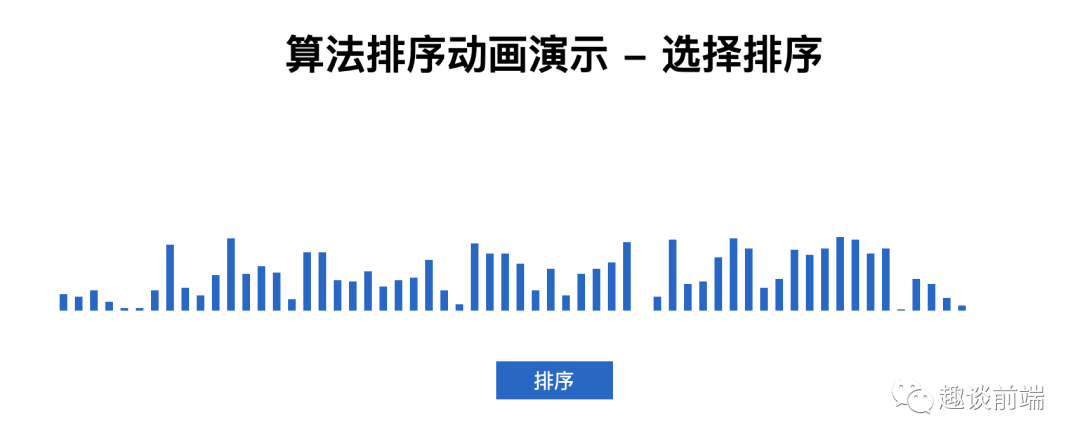
選擇排序代碼如下:

selectionSort(arr) {
    let len = arr.length,
        indexMin
    for(let i = 0; i< len -1; i++) {
      indexMin = i
      for(let j = i; j < len; j++){
        if(arr[indexMin] > arr[j]) {
          indexMin = j
        }
      }
      if(i !== indexMin) {
        [arr[i], arr[indexMin]] = [arr[indexMin], arr[i]]
      }
    }
    return arr
}

點擊排序時, 結(jié)果如下:

說明代碼運行正常, 可以實現(xiàn)排序, 控制臺耗時為: 0.13720703125ms, 明顯比冒泡排序性能要好.

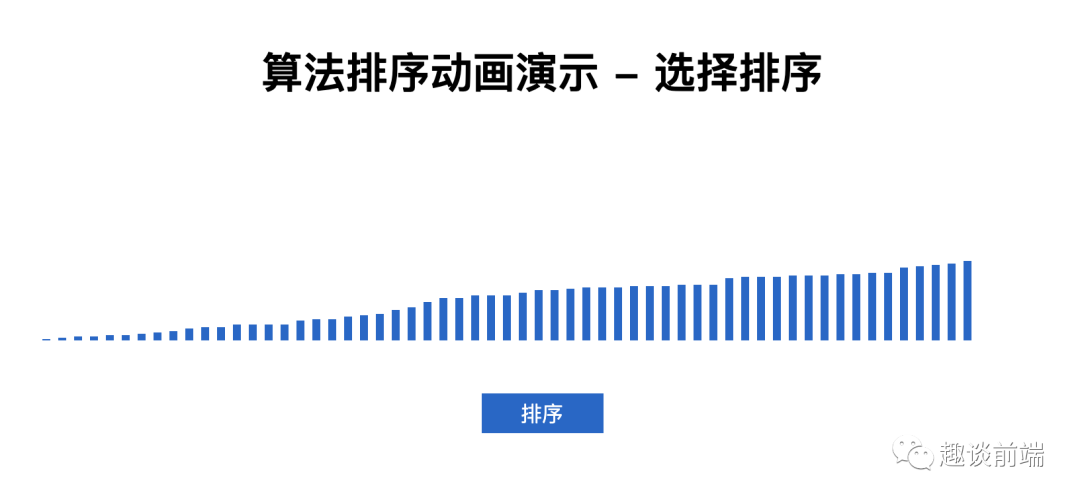
3. 插入排序

插入排序?的思路是每次排一個數(shù)組項,假定第一項已經(jīng)排序,接著它和第二項比較, 決定第二項的位置, 然后接著用同樣的方式?jīng)Q定第三項的位置, 依次類推, 最終將整個數(shù)組從小到大依次排序.

代碼如下:

insertionSort(arr) {
    let len = arr.length,
        j,
        temp;
    for(let i = 1; i< len; i++) {
      j = i
      temp = arr[i]
      while(j > 0 && arr[j-1] > temp) {
        arr[j] = arr[j-1]
        j--
      }
      arr[j] = temp;
    }
 }

執(zhí)行結(jié)果如下:

控制臺打印耗時為:0.09912109375ms.

4. 歸并排序

歸并排序算法性能比以上三者都好, 可以在實際項目中投入使用,但實現(xiàn)方式相對復(fù)雜.

歸并排序是一種分治算法,其思想是將原始數(shù)組切分成較小的數(shù)組，直到每個小數(shù)組只有一個元素，接著將小數(shù)組歸并成較大的數(shù)組，最后變成一個排序完成的大數(shù)組。

其實現(xiàn)過程如下圖所示：

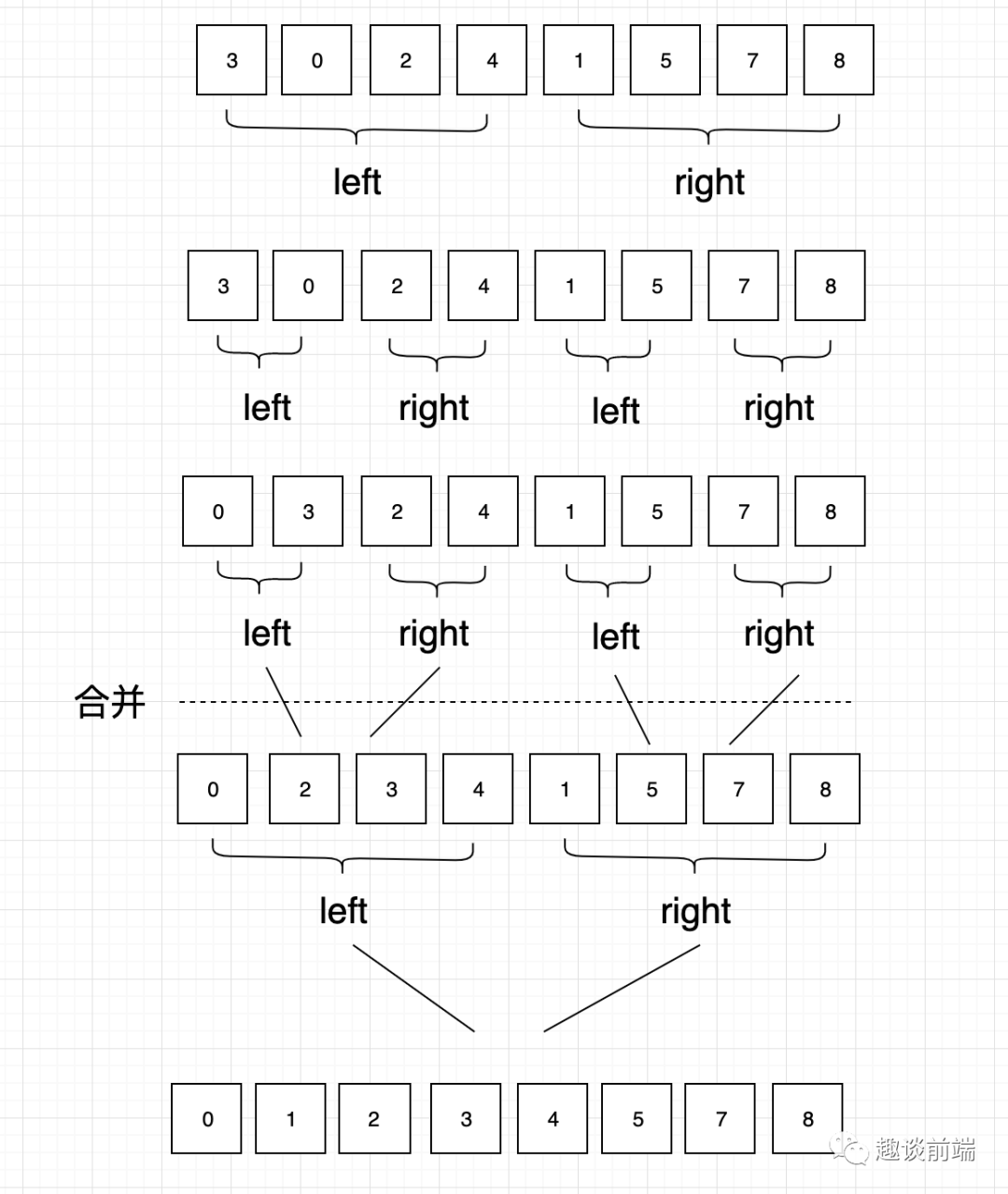
為了實現(xiàn)該方法我們需要準備一個合并函數(shù)和一個遞歸函數(shù)，具體實現(xiàn)如下代碼：

// 歸并排序
mergeSortRec(arr) {
 let len = arr.length
 if(len === 1) {
   return arr
 }
 let mid = Math.floor(len / 2),
     left = arr.slice(0, mid),
     right = arr.slice(mid, len)
 return merge(mergeSortRec(left), mergeSortRec(right))
}
// 合并方法
merge(left, right) {
    let result = []
        l = 0,
        r = 0;
    while(l < left.length && r < right) {
      if(left[l] < right(r)) {
        result.push(left[l++])
      }else {
        result.push(right[r++])
      }
    }
    while(l < left.length) {
      result.push(left[l++])
    }
    while(r < right.length) {
      result.push(right[r++])
    }
    return result
}

以上代碼中的遞歸作用是將一個大數(shù)組劃分為多個小數(shù)組直到只有一項，然后再逐層進行合并排序。如果有不理解的可以和筆者交流或者結(jié)合筆者畫的草圖進行理解。

5. 快速排序

快速排序是目前比較常用的排序算法，它的復(fù)雜度為O(nlog^n),并且它的性能比其他復(fù)雜度為O(nlog^n)的好，也是采用分治的思想，將原始數(shù)組進行劃分，由于快速排序?qū)崿F(xiàn)起來比較復(fù)雜，這里講一下思路：

1. 從數(shù)組中選擇中間項作為主元
2. 創(chuàng)建兩個指針，左邊一個指向數(shù)組第一項，右邊一個指向數(shù)組最后一項，移動左指針直到我們找到一個比主元大的元素，移動右指針直到找到一個比主元小的元素，然后交換它們的位置，重復(fù)此過程直到左指針超過了右指針
3. 算法對劃分后的小數(shù)組重復(fù)1，2步驟，直到數(shù)組完全排序完成。

代碼如下：

// 快速排序
quickSort(arr, left, right) {
    let index
    if(arr.length > 1) {
      index = partition(arr, left, right)
      if(left < index - 1) {
        quickSort(arr, left, index -1)
      }
      if(index < right) {
        quickSort(arr, index, right)
      }
    }
  }
// 劃分流程
partition(arr, left, right) {
    let part = arr[Math,floor((right + left) / 2)],
        i = left,
        j = right
    while(i <= j) {
      while(arr[i] < part) {
        i++
      }
      while(arr[j] > part) {
        j--
      }
      if(i <= j) {
        // 置換
        [arr[i], arr[j]] = [arr[j], arr[i]]
        i++
        j--
      }
    }
    return i
}

7. 順序搜索

搜索算法也是我們經(jīng)常用到的算法之一，比如我們需要查找某個用戶或者某條數(shù)據(jù)，不管是在前端還是在后端，都會使用搜索算法。我們先來介紹最簡單也是效率最低的順序搜索，其主要思想是將每一個數(shù)據(jù)結(jié)構(gòu)中的元素和我們要查詢的元素做比較，然后返回指定元素的索引。

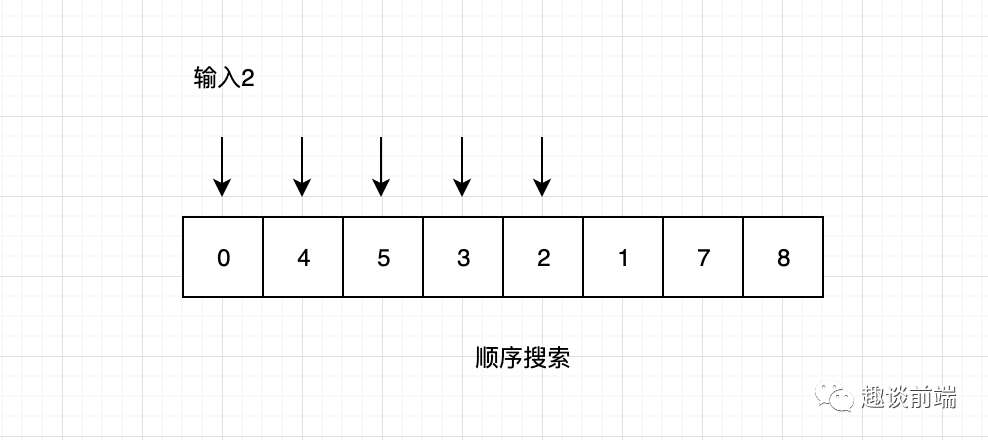
之所以說順序搜索效率低是因為每次都要從數(shù)組的頭部開始查詢，直到查找到要搜索的值，整體查詢不夠靈活和動態(tài)性。順序搜索代碼實現(xiàn)如下：

sequentialSearch(arr, item) {
    for(let i = 0; i< arr.length; i++) {
      if(item === arr[i]) {
        return i
      }
    }
    return -1
}

接下來我們看下面一種比較常用和靈活的搜索算法——二分搜索。

8. 二分搜索

二分搜索的思想有點“投機學(xué)”的意思，但是它是一種有理論依據(jù)的“投機學(xué)”。首先它要求被搜索的數(shù)據(jù)結(jié)構(gòu)已排序，其次進行如下步驟：

1. 找出數(shù)組的中間值
2. 如果中間值是待搜索的值，那么直接返回中間值的索引
3. 如果待搜索的值比中間值小，則返回步驟1，將區(qū)間范圍縮小，在中間值左邊的子數(shù)組中繼續(xù)搜索
4. 如果待搜索的值比選中的值大，則返回步驟1，將區(qū)間范圍縮小，在中間值右邊的子數(shù)組中繼續(xù)搜索
5. 如果沒有搜到，則返回-1

為了方便理解筆者畫了如下草圖：

由上圖大家可以很容易的理解二分搜索的實現(xiàn)過程，接下來我們看下代碼實現(xiàn)：

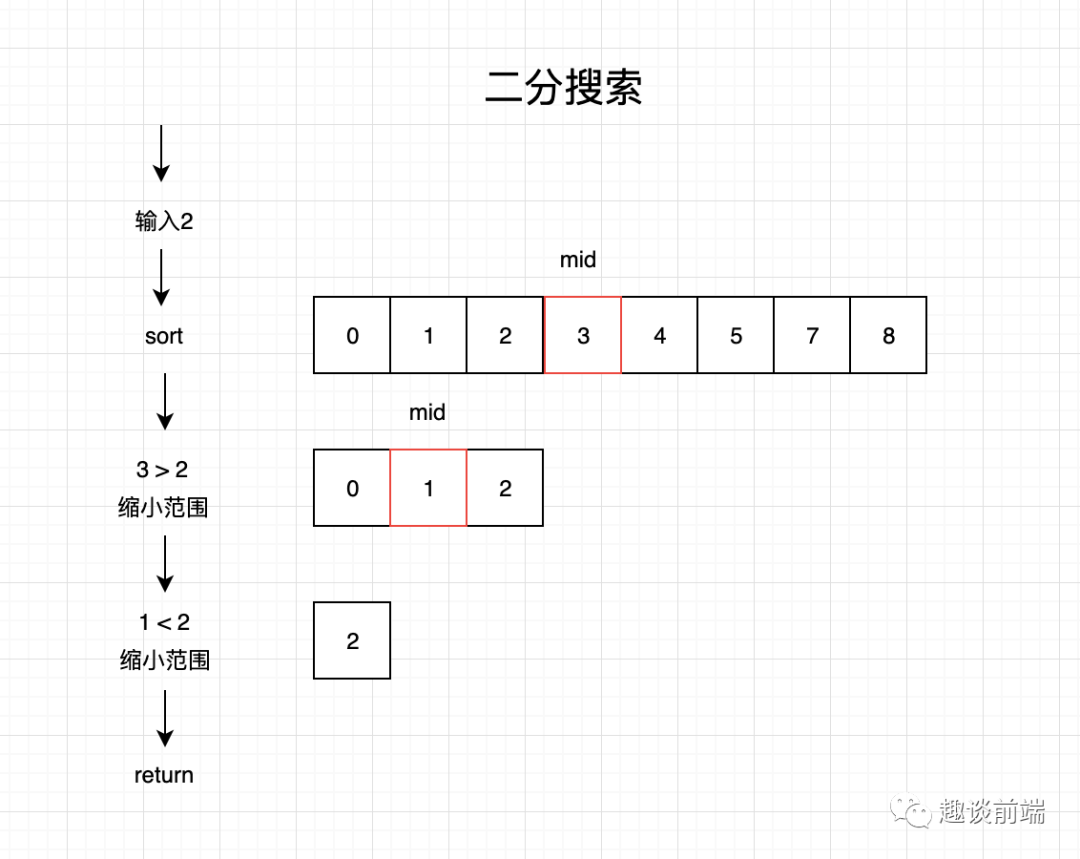
binarySearch(arr, item) {
    // 調(diào)用排序算法先對數(shù)據(jù)進行排序
    this.quickSort(arr)

    let min = 0,
        max = arr.length - 1,
        mid,
        el
    while(min <= max) {
      mid = Math.floor((min + max) / 2)
      el = arr[mid]
      if(el < item) {
        min = mid + 1
      }else if(el > item) {
        max = mid -1
      }else {
        return mid
      }
    }
    return -1
  }

其實還有很多搜索算法，筆者在js基本搜索算法實現(xiàn)與170萬條數(shù)據(jù)下的性能測試有具體介紹。

參考文獻：Learning JavaScript Data Structures and Algorithms

更多推薦

前端推薦!3分鐘帶你了解開源圖片編輯器iDraw.js

推薦!使用H5-Dooring快速搭建智能汽車移動端站點

lerna + dumi + eslint多包管理實踐

動態(tài)刻度可視化組件實現(xiàn)

從零開發(fā)一款輕量級滑動驗證碼插件(深度復(fù)盤)

從零搭建全棧可視化大屏制作平臺V6.Dooring