【機(jī)器學(xué)習(xí)筆記】:從零開始學(xué)會(huì)邏輯回歸(一)
↑ 關(guān)注 + 星標(biāo) ,每天學(xué)Python新技能
后臺(tái)回復(fù)【大禮包】送你Python自學(xué)大禮包
作者:xiaoyu
知乎:https://zhuanlan.zhihu.com/pypcfx
介紹:一個(gè)半路轉(zhuǎn)行的數(shù)據(jù)挖掘工程師
▍前言
邏輯回歸是一個(gè)非常經(jīng)典,也是很常用的模型。之前和大家分享過它的重要性:5個(gè)原因告訴你:為什么在成為數(shù)據(jù)科學(xué)家之前,“邏輯回歸”是第一個(gè)需要學(xué)習(xí)的
關(guān)于邏輯回歸,可以用一句話來總結(jié):邏輯回歸假設(shè)數(shù)據(jù)服從伯努利分布,通過極大似然函數(shù)的方法,運(yùn)用梯度下降來求解參數(shù),來達(dá)到將數(shù)據(jù)二分類的目的。
本篇我們就開始邏輯回歸的介紹。
▍sigmoid函數(shù)
首先我們了解一個(gè)函數(shù):sigmoid,邏輯回歸就是基于這個(gè)函數(shù)構(gòu)建的模型。sigmod函數(shù)公式如下:

使用Python的numpy,matplotlib對(duì)該函數(shù)進(jìn)行可視化,如下:
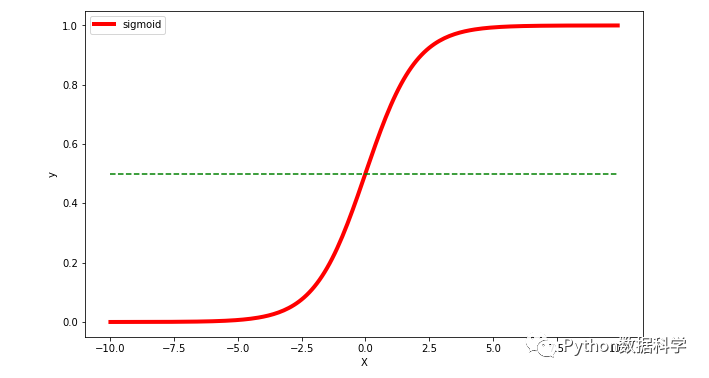
圖中我們可以直觀地看到這個(gè)函數(shù)的一些特點(diǎn):
中間范圍內(nèi)函數(shù)斜率最大,對(duì)應(yīng)Y的大部分?jǐn)?shù)值變化
Y軸數(shù)值范圍在 0~1 之間
X軸數(shù)值范圍沒有限制,但當(dāng)X大于一定數(shù)值后,Y無限趨近于1,而小于一定數(shù)值后,Y無限趨近于0
特別地,當(dāng) X=0 時(shí),Y=0.5
▍廣義線性模型
前幾篇我們?cè)敿?xì)地介紹了線性回歸模型:
其中在殘差分析的過程中,如果殘差方差不是齊性的,我們一般會(huì)對(duì)變量取自然對(duì)數(shù)進(jìn)行變換,以達(dá)到殘差方差齊性的效果。比如我們這樣取對(duì)數(shù):
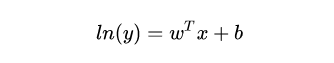
我們一般稱這種為“對(duì)數(shù)線性回歸”,其形式上是線性回歸,但實(shí)際上是在求輸入空間到輸出空間的非線性函數(shù)映射。這里的對(duì)數(shù)函數(shù)就起到了將線性回歸模型預(yù)測(cè)值與真實(shí)值聯(lián)系起來的作用。
我們稱這樣變換后的模型為“廣義線性模型”,其中對(duì)數(shù)函數(shù)為“聯(lián)系函數(shù)”,當(dāng)然也可以是其他函數(shù)。廣義線性模型是個(gè)宏觀概念,上面通過對(duì)數(shù)函數(shù)變換得到的模型只是廣義線性模型的其中一種而已。
▍邏輯回歸模型構(gòu)建
了解了上面的基本內(nèi)容,我們來看一下邏輯回歸模型是如何建立的。其實(shí),邏輯回歸模型也是廣義線性模型的其中一種,只是形式上和上面取對(duì)數(shù)有些不同。它正是通過開始提到的sigmoid函數(shù)變換得到的模型。
那么為什么要用sigmoid函數(shù)呢?
對(duì)于一般的線性回歸模型,我們知道:我們的自變量X和因變量Y都是連續(xù)的數(shù)值,通過X的輸入就可以很好的預(yù)測(cè)Y值。
但現(xiàn)實(shí)生活中,我們也有離散的數(shù)據(jù)類型,比如好和壞,男和女等等。那么我們?cè)谙耄涸诰€性回歸模型的基礎(chǔ)上,是否可以實(shí)現(xiàn)一個(gè)預(yù)測(cè)因變量是離散數(shù)據(jù)類型的模型呢?
答案當(dāng)然是可以的。我們可能會(huì)想到階躍函數(shù):
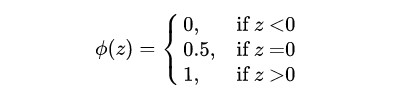
但是它在這里是不合適的,正如我們神經(jīng)網(wǎng)絡(luò)激活函數(shù)不選擇階躍函數(shù)一樣,因?yàn)樗?strong>不連續(xù)不可微。而能滿足分類效果,且是連續(xù)的函數(shù),sigmoid是再好不過的選擇了(返回文章開頭看一下sigmoid函數(shù)的特點(diǎn)就知道了)。因此,邏輯回歸模型就可以通過在線性回歸模型的基礎(chǔ)上,套一個(gè)sigmoid函數(shù)來實(shí)現(xiàn),這樣不管X取什么樣的值,Y值都被非線性地映射在 0~1 之間,實(shí)現(xiàn)二分類。這也證明一個(gè)結(jié)論:邏輯回歸不是回歸模型,而是分類模型。
我們這里討論的都是二元分類,因此,一個(gè)二元邏輯回歸模型就建立出來了,其的公式如下:

我們簡(jiǎn)單地把原來的X替換為一個(gè)線性模型就得到了上面公式。代替部分可以擴(kuò)展如下:
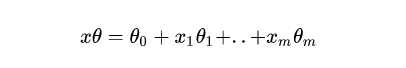
除了上面的表現(xiàn)形式,我們也可以用另外一種形式來表達(dá)二元邏輯回歸模型。將上面模型簡(jiǎn)單地進(jìn)行變化:

公式中,y可以理解為樣本x為正例的概率,而1-y則可以理解為樣本x為負(fù)例時(shí)的概率。二者的比值y/(1-y)被稱為“odds”,即“幾率”,反映了x作為正例的相對(duì)可能性,對(duì)幾率取對(duì)數(shù)就得到了線性回歸模型了。
上式其實(shí)是在用線性回歸模型的預(yù)測(cè)結(jié)果去逼近真實(shí)標(biāo)記的對(duì)數(shù)幾率。所以該模型也被稱作“對(duì)數(shù)幾率回歸”。
▍二元邏輯回歸是如何進(jìn)行分類的?
通過上面的介紹,我們知道了二元邏輯回歸的模型。但我們發(fā)現(xiàn)它的Y是在 0~1 之間連續(xù)的數(shù)值,也即這個(gè)范圍內(nèi)的任意小數(shù)(百分比)。那么這些小數(shù)是如何進(jìn)行分類的呢?
可以將模型的輸出h(x)當(dāng)作某一分類的概率的大小。這樣來看,小數(shù)值越接近1,說明是1分類的概率越大,相反,小數(shù)值越接近0,說明是0分類的概率越大。
而實(shí)際使用中,我們會(huì)對(duì)所有輸出結(jié)果進(jìn)行排序,然后結(jié)合業(yè)務(wù)來決定出一個(gè)閾值。假如閾值是0.5,那么我們就可以將大于0.5的輸出都視為1分類,而小于0.5的輸出都視為0分類。所以,二元邏輯回歸是一種概率類模型,是通過排序并和閾值比較進(jìn)行分類的。
這個(gè)閾值的選擇關(guān)系到評(píng)估標(biāo)準(zhǔn)的結(jié)果,其實(shí)我們之前也提到過。ROC曲線就是通過遍歷所有閾值來實(shí)現(xiàn)的,曲線上每一個(gè)點(diǎn)對(duì)應(yīng)一對(duì)FPR和TPR,而FPR和TPR平衡的點(diǎn)即為F分?jǐn)?shù)【機(jī)器學(xué)習(xí)筆記】:一文讓你徹底記住什么是ROC/AUC(看不懂你來找我)
▍邏輯回歸的假設(shè)
正如線性回歸模型一樣,邏輯回歸也有假設(shè)條件,主要是兩個(gè):
(1)假設(shè)數(shù)據(jù)服從伯努利分布
(2)假設(shè)模型的輸出值是樣本為正例的概率
基于這兩個(gè)假設(shè),我們可以分別得出類別為1和0的后驗(yàn)概率估計(jì):
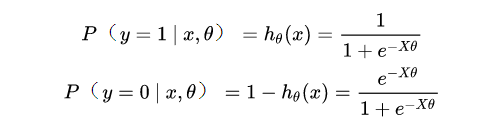
▍邏輯回歸的損失函數(shù)
有了模型,我們自然會(huì)想到要求策略,也就是損失函數(shù)。對(duì)于邏輯回歸,我們很自然想到:用線性回歸的損失函數(shù)“離差平方和”的形式是否可以?
但事實(shí)上,這種形式并不適合,因?yàn)樗煤瘮?shù)并非凸函數(shù),而是有很多局部的最小值,這樣不利于求解。
前面說到邏輯回歸其實(shí)是概率類模型,因此,我們通過極大似然估計(jì)(MLE)推導(dǎo)邏輯回歸損失函數(shù)。下面是具體推導(dǎo)過程。
上面我們通過基本假設(shè)得到了1和0兩類的后驗(yàn)概率,現(xiàn)在將兩個(gè)概率合并可得:
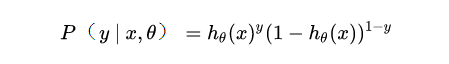
現(xiàn)在我們得到了模型概率的一般形式,接下來就可以使用極大似然估計(jì)來根據(jù)給定的訓(xùn)練集估計(jì)出參數(shù),將n個(gè)訓(xùn)練樣本的概率相乘得到:
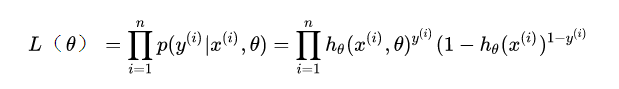
似然函數(shù)是相乘的模型,我們可以通過取對(duì)數(shù)將等式右側(cè)變?yōu)橄嗉幽P停缓髮⒅笖?shù)提前,以便于求解。變換后如下:
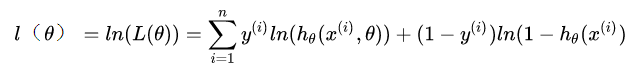
如此就推導(dǎo)出了參數(shù)的最大似然估計(jì)。我們的目的是將所得似然函數(shù)極大化,而損失函數(shù)是最小化,因此,我們需要在上式前加一個(gè)負(fù)號(hào)便可得到最終的損失函數(shù)。
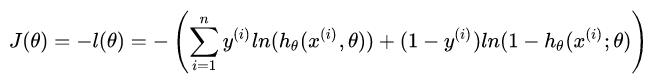

其等價(jià)于:
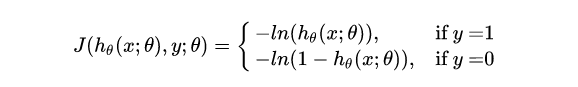
注:邏輯回歸的損失函數(shù)“對(duì)數(shù)似然函數(shù)”,在模型GBDT分類情況下也會(huì)用到,又叫作“交叉熵”。
▍邏輯回歸損失函數(shù)求解
現(xiàn)在我們推導(dǎo)出了邏輯回歸的損失函數(shù),而需要求解是模型的參數(shù)theta,即線性模型自變量的權(quán)重系數(shù)。對(duì)于線性回歸模型而言,可以使用最小二乘法,但對(duì)于邏輯回歸而言使用傳統(tǒng)最小二乘法求解是不合適的。
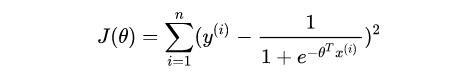
邏輯回歸的最小二乘法的代價(jià)函數(shù)
對(duì)于不適合的解釋原因有很多,但本質(zhì)上不能使用經(jīng)典最小二乘法的原因在于:logistic回歸模型的參數(shù)估計(jì)問題不能“方便地”定義“誤差”或者“殘差”。
因此,考慮使用迭代類算法優(yōu)化,常見的就是”梯度下降法“。當(dāng)然,還有其它方法比如,坐標(biāo)軸下降法,牛頓法等。我們本篇介紹使用”梯度下降法“來對(duì)損失函數(shù)求解。
使用梯度下降法求解邏輯回歸損失函數(shù)。梯度下降的迭代公式如下:
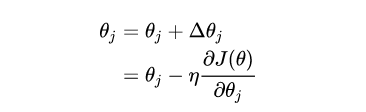
問題變?yōu)槿绾吻髶p失函數(shù)對(duì)參數(shù)theta的梯度。下面進(jìn)行詳細(xì)推導(dǎo)過程:
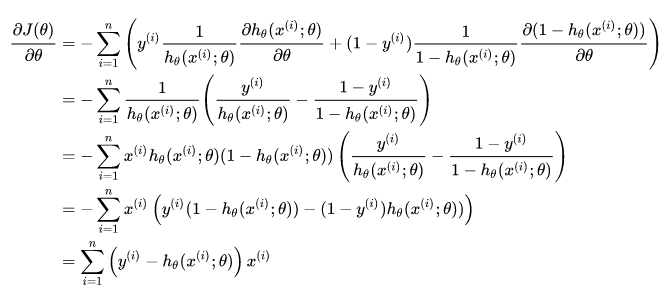
推導(dǎo)過程中需要用到的數(shù)學(xué)知識(shí)是:偏導(dǎo),對(duì)數(shù)求導(dǎo),sigmoid函數(shù)求導(dǎo)。其中,函數(shù)求導(dǎo)公式如下:
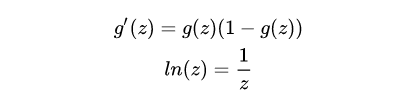
最后將求得的梯度帶入迭代公式中,即為:
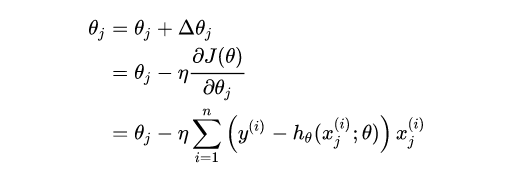
注意:公式中,i 代表樣本數(shù),j 代表特征數(shù)。
其實(shí),常用梯度下降有三個(gè)種方法,可以根據(jù)需要選擇,分別是:批量梯度下降(BGD),隨機(jī)梯度下降(SGD),small batch梯度下降。具體不進(jìn)行介紹。
▍邏輯回歸的優(yōu)缺點(diǎn)
優(yōu)點(diǎn):
1. 直接對(duì)分類可能性進(jìn)行建模,無需實(shí)現(xiàn)假設(shè)數(shù)據(jù)分布,這樣就避免了假設(shè)分布不準(zhǔn)確所帶來的問題。
2. 形式簡(jiǎn)單,模型的可解釋性非常好,特征的權(quán)重可以看到不同的特征對(duì)最后結(jié)果的影響。
3. 除了類別,還能得到近似概率預(yù)測(cè),這對(duì)許多需利用概率輔助決策的任務(wù)很有用。
缺點(diǎn):
1. 準(zhǔn)確率不是很高,因?yàn)樾蝿?shì)非常的簡(jiǎn)單,很難去擬合數(shù)據(jù)的真實(shí)分布。
2. 本身無法篩選特征。
以上就是關(guān)于邏輯回歸模型的一些分享,還有其它正則化,多元邏輯回歸等問題,我們將在后續(xù)進(jìn)行介紹。另外,后續(xù)也將準(zhǔn)備邏輯回歸sklearn的使用和實(shí)戰(zhàn)練習(xí)。
如果有任何問題,歡迎指正和補(bǔ)充,
另外歡迎點(diǎn)贊和轉(zhuǎn)發(fā)支持!
參考:
機(jī)器學(xué)習(xí),周志華
https://blog.csdn.net/yinyu19950811/article/details/81321944
https://www.cnblogs.com/pinard/p/6029432.html
推薦閱讀
推薦一個(gè)公眾號(hào),幫助程序員自學(xué)與成長(zhǎng)
覺得還不錯(cuò)就給我一個(gè)小小的鼓勵(lì)吧!


