【機器學(xué)習(xí)】關(guān)于邏輯回歸，面試官都怎么問

作者 | Chilia     

整理 | NewBeeNLP

最近準備開始如同考研一般的秋招復(fù)習(xí)了！感覺要復(fù)習(xí)的東西真的是浩如煙海;) 有2023屆做算法的同學(xué)可以加入我們一起復(fù)習(xí)~

1. 介紹

邏輯回歸假設(shè)數(shù)據(jù)服從「伯努利分布」(因為是二分類),通過「極大化似然函數(shù)」的方法，運用梯度下降來求解參數(shù)，來達到將數(shù)據(jù)二分類的目的。

決策函數(shù)

設(shè)「x」是m維的樣本特征向量(input)；y是標(biāo)簽label，為正例和負例。這里 是模型參數(shù)，也就是回歸系數(shù)。則該樣本是正例的概率為：

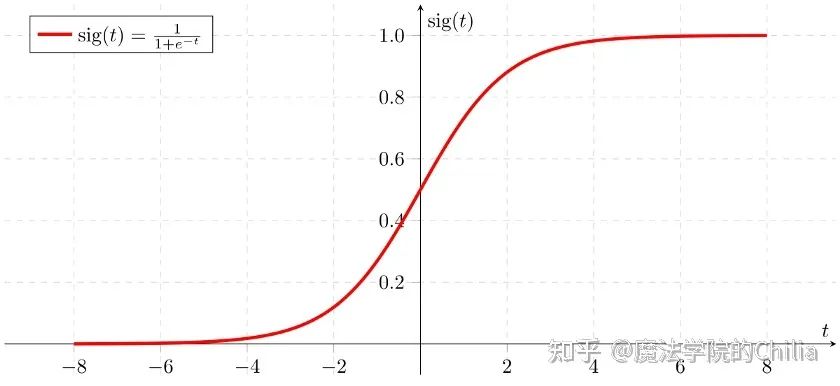
這里使用sigmoid函數(shù)的目的是為了把普通的線性回歸問題轉(zhuǎn)化為輸出為[0,1]區(qū)間的二分類問題。

損失函數(shù)

在統(tǒng)計學(xué)中，常常使用極大似然估計法來求解參數(shù)。即找到一組參數(shù)，使得在這組參數(shù)下，我們的數(shù)據(jù)的似然度（概率）最大。

設(shè)：

那么，似然函數(shù)為：

為了更方便求解，我們對等式兩邊同取對數(shù)，寫成「對數(shù)似然函數(shù)」：

從另一個角度來講，對于一個樣本來說，它的「交叉熵損失函數(shù)」為：

所有樣本的交叉熵損失函數(shù)為：

這就是對數(shù)似然函數(shù)取相反數(shù)嘛！所以，在邏輯回歸模型中，「最大化對數(shù)似然函數(shù)和最小化損失函數(shù)實際上是等價的」。

梯度下降求解

對一個樣本做梯度下降，

并行化

LR的一個好處就是它能夠并行化，效率很高。使用小批量梯度下降：

這些操作均可用矩陣運算來并行解決。

2. 常見面試題

Q1: LR與線性回歸的區(qū)別與聯(lián)系

邏輯回歸是一種廣義線性模型，它引入了Sigmoid函數(shù)，是非線性模型，但本質(zhì)上還是一個線性回歸模型，因為除去Sigmoid函數(shù)映射關(guān)系，其他的算法都是線性回歸的。

邏輯回歸和線性回歸首先都是廣義的線性回歸，在本質(zhì)上沒多大區(qū)別，區(qū)別在于邏輯回歸多了個Sigmoid函數(shù)，使樣本映射到[0,1]之間的數(shù)值，從而來處理分類問題。另外邏輯回歸是假設(shè)變量服從伯努利分布，線性回歸假設(shè)變量服從高斯分布。邏輯回歸輸出的是離散型變量，用于分類，線性回歸輸出的是連續(xù)性的，用于預(yù)測。邏輯回歸是用最大似然法去計算預(yù)測函數(shù)中的最優(yōu)參數(shù)值，而線性回歸是用最小二乘法去對自變量量關(guān)系進行擬合。

Q2: 連續(xù)特征的離散化：在什么情況下將連續(xù)的特征離散化之后可以獲得更好的效果？例如CTR預(yù)估中，特征大多是離散的，這樣做的好處在哪里？

答：在工業(yè)界，很少直接將連續(xù)值作為邏輯回歸模型的特征輸入，而是將連續(xù)特征離散化為一系列0、1特征交給邏輯回歸模型，這樣做的優(yōu)勢有以下幾點：

• 離散特征的增加和減少都很容易，易于模型的快速迭代，容易擴展；
• 離散化后的特征對異常數(shù)據(jù)有很強的魯棒性：比如一個特征是年齡>30是1，否則0。如果特征沒有離散化，一個異常數(shù)據(jù)“年齡300歲”會給模型造成很大的干擾；
• 邏輯回歸屬于廣義線性模型，表達能力受限；單變量離散化為N個后，每個變量有單獨的權(quán)重，相當(dāng)于為模型引入了非線性，能夠提升模型表達能力，加大擬合。具體來說，離散化后可以進行特征交叉，由M+N個變量變?yōu)镸*N個變量；
• 特征離散化后，模型會更穩(wěn)定，比如如果對用戶年齡離散化，20-30作為一個區(qū)間，不會因為一個用戶年齡長了一歲就變成一個完全不同的人。當(dāng)然處于區(qū)間相鄰處的樣本會剛好相反，所以怎么劃分區(qū)間是門學(xué)問。

Q3：邏輯回歸在訓(xùn)練的過程當(dāng)中，如果有很多的特征高度相關(guān)，或者說有一個特征重復(fù)了100遍，會造成怎樣的影響？

先說結(jié)論，如果在損失函數(shù)最終收斂的情況下，其實就算有很多特征高度相關(guān)也不會影響分類器的效果。可以認為這100個特征和原來那一個特征扮演的效果一樣，只是可能中間很多特征的值正負相消了。

為什么我們還是會在訓(xùn)練的過程當(dāng)中將高度相關(guān)的特征去掉？

• 去掉高度相關(guān)的特征會讓模型的可解釋性更好
• 可以大大提高訓(xùn)練的速度。如果模型當(dāng)中有很多特征高度相關(guān)的話，就算損失函數(shù)本身收斂了，但實際上參數(shù)是沒有收斂的，這樣會拉低訓(xùn)練的速度。其次是特征多了，本身就會增大訓(xùn)練的時間。