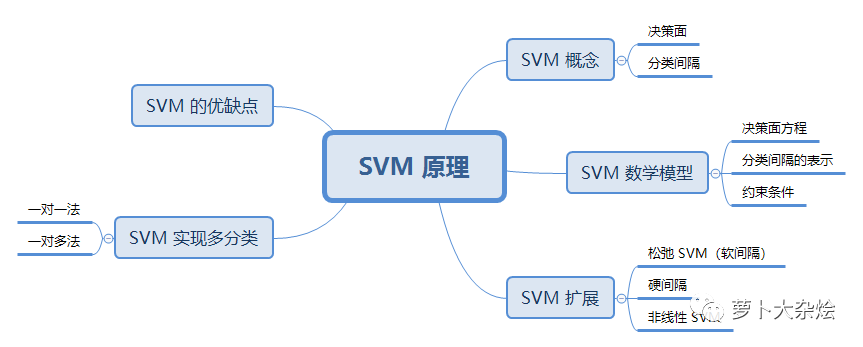
數(shù)據(jù)分析入門(mén)系列教程-SVM原理
SVM 的英文全稱是 Support Vector Machines,我們叫它支持向量機(jī),支持向量機(jī)是用于分類的一種算法,當(dāng)然也有人用它來(lái)做回歸。

SVM 原理
我們先通過(guò)一個(gè)分類的例子來(lái)看一下 SVM 的定義
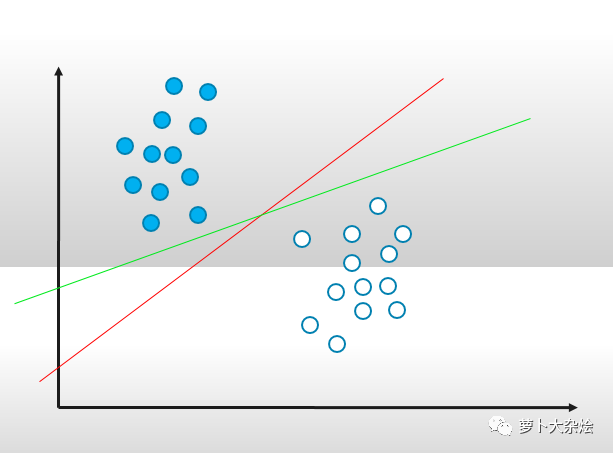
在一個(gè)二維平面上,有實(shí)心和空心兩組圓點(diǎn),如果我們想用一條線分開(kāi)它們,那么其實(shí)可以畫(huà)出無(wú)數(shù)條這種區(qū)分線。
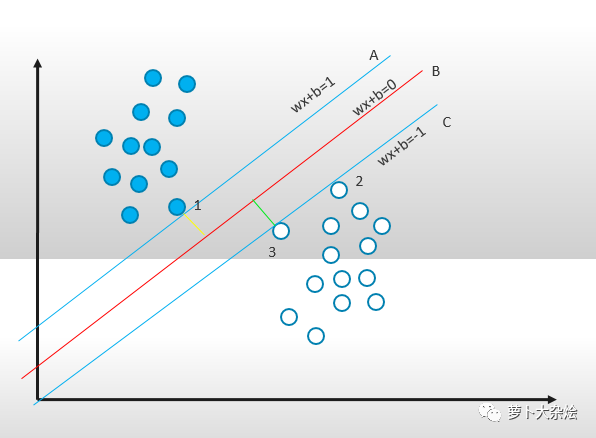
而 SVM 就是試圖把線放在最佳位置,好讓在線的兩邊到兩組圓點(diǎn)邊界點(diǎn)的距離盡可能大。體現(xiàn)在圖上就是:
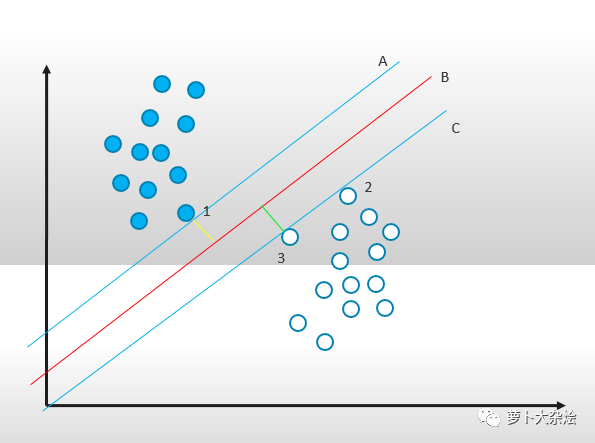
線 A 正好緊挨實(shí)心點(diǎn)的最邊界點(diǎn),線 C 正好緊挨空心點(diǎn)的最邊界點(diǎn),而線 A,B,C是三條平行線且線 B 處于線 A 和 C 距離的中心處,且圖中的綠線和黃線為最大距離,則此時(shí)的線 B 即為支持向量機(jī)算法下的最優(yōu)解。而點(diǎn)1,2,3就稱為支持向量,即 support vector。
當(dāng)然,還可以擴(kuò)展到三維空間中,那么就是使用平面進(jìn)行分割
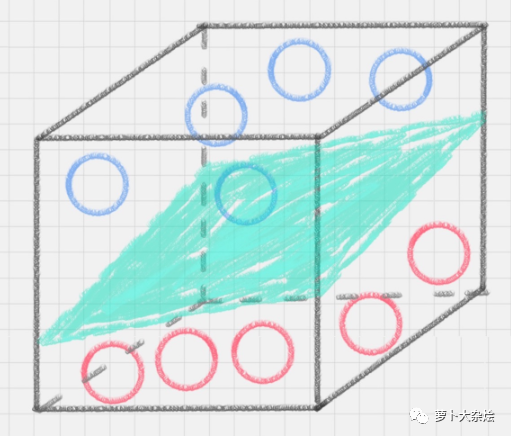
此時(shí)我們也稱線 B 或者三維中的綠色平面為“決策面”。
決策面和分類間隔
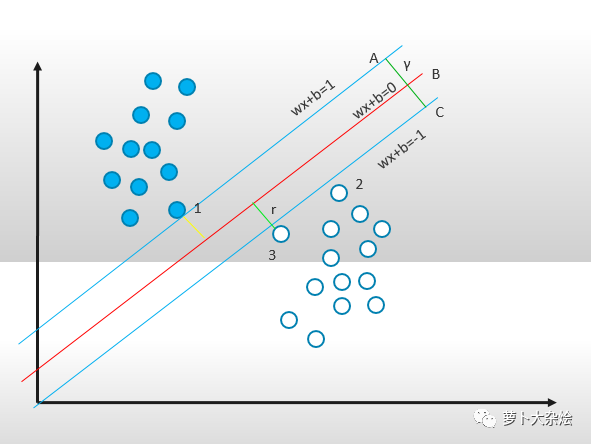
在保證決策面方向不變且不會(huì)出現(xiàn)錯(cuò)分樣本的情況下移動(dòng)決策面,會(huì)在原來(lái)的決策面兩側(cè)找到兩個(gè)極限位置(越過(guò)該位置就會(huì)產(chǎn)生錯(cuò)分現(xiàn)象),如圖中的兩條藍(lán)線。藍(lán)線的位置由決策面的方向和距離原決策面最近的幾個(gè)樣本的位置決定(即黃線和綠線)。而這兩條平行藍(lán)線正中間的分界線就是在保持當(dāng)前決策面方向不變的前提下的最優(yōu)決策面。兩條藍(lán)線之間的垂直距離就是這個(gè)最優(yōu)決策面對(duì)應(yīng)的分類間隔。這個(gè)具有“最大間隔”的決策面就是 SVM 要尋找的最優(yōu)解。而這個(gè)真正的最優(yōu)解對(duì)應(yīng)的兩側(cè)藍(lán)線所穿過(guò)的樣本點(diǎn),就是 SVM 中的支持樣本點(diǎn),稱為“支持向量”,這個(gè)概念我們上面也提到了。
由上面的圖示可以看出,要想找到最優(yōu)的決策面,其實(shí)就是一個(gè)求解最優(yōu)的問(wèn)題,即最優(yōu)化問(wèn)題。
當(dāng)然以上我們討論的都屬于線性的 SVM,對(duì)于非線性問(wèn)題,在后面再做討論
線性 SVM 數(shù)學(xué)建模
下面我們就來(lái)看看如何使用數(shù)學(xué)公式來(lái)表示 SVM
在一個(gè)最優(yōu)化問(wèn)題中,一般有兩個(gè)最基本的因素需要解決:
目標(biāo)函數(shù),就是我們希望什么東西的什么達(dá)到最好。
優(yōu)化對(duì)象,就是我們希望通過(guò)改變哪些因素來(lái)使目標(biāo)函數(shù)達(dá)到最優(yōu)
在 SVM 算法中,目標(biāo)函數(shù)對(duì)應(yīng)的應(yīng)該是“分類間隔”,因?yàn)槲覀兿M鶕?jù) SVM 的定義,我們需要找到這個(gè)最大的距離,才是 SVM 的最優(yōu)解。而優(yōu)化對(duì)象就是決策面,我們需要移動(dòng)決策面的位置和方向,來(lái)使得分類間隔達(dá)到最大。
決策面方程
這里我們考慮的是一個(gè)兩類的分類問(wèn)題,數(shù)據(jù)點(diǎn)用 x 來(lái)表示,這是一個(gè) n 維向量,而類別用 y 來(lái)表示,可以取 1 或者 -1 ,分別代表兩個(gè)不同的類(這里類別用1和-1就是為了 SVM 公式的推導(dǎo))。一個(gè)線性分類器就是要在 n 維的數(shù)據(jù)空間中找到一個(gè)超平面,其方程可以表示為
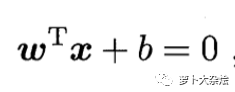
一個(gè)超平面,在二維空間中的例子就是一條直線。我們希望的是,通過(guò)這個(gè)超平面可以把兩類數(shù)據(jù)分隔開(kāi)來(lái),比如,在超平面一邊的數(shù)據(jù)點(diǎn)所對(duì)應(yīng)的 y 全是 -1 ,而在另一邊全是 1 。
這里的 w 和 x 都是向量,因?yàn)橄蛄磕J(rèn)都是列向量,所以把 w 轉(zhuǎn)置一下就變成行向量了,然后它們的乘積就是一個(gè)標(biāo)量,這樣就可以達(dá)到加一個(gè)標(biāo)量 y 使得結(jié)果為0。
分類間隔
分類間隔說(shuō)白了,就是點(diǎn)到直線的距離,公式為:
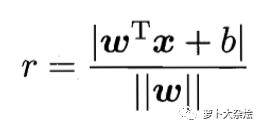
||w|| 就是向量 w 的模,即向量的長(zhǎng)度;x 就是支持向量樣本點(diǎn)的坐標(biāo);y 等同于決策面方程中的 y。
SVM 約束條件
我們假設(shè)超平面(w, b)可以將訓(xùn)練樣本完全正確的分類,所以如果類別 y = 1,則有 wx + b > 0,如果 y = -1,則有 wx + b < 0。此時(shí)再根據(jù) SVM 的定義,要想正確分類,我們需要有如下約束:
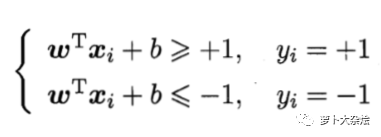
記為約束條件1
由因?yàn)閮蓷l邊界線(藍(lán)線)之間的距離 y 等于 2r,而此時(shí) wx + b 是等于1的,所以可以得到 γ 的距離為
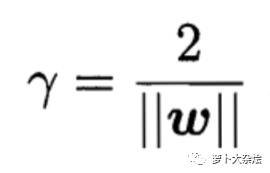
此時(shí)求解最優(yōu) SVM 就變成了求解在約束條件1下的 γ 的最大值,
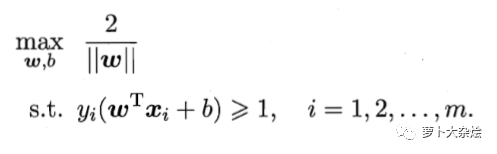
注意因?yàn)轭悇e y 和 wx + b 是同號(hào)的,所以它們的乘積永遠(yuǎn)為正數(shù)
也即是求 ||w|| 的最小化,即:
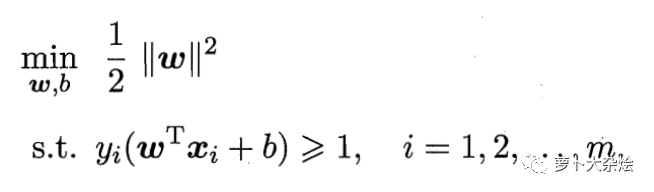
這個(gè)就是支持向量機(jī)的基本數(shù)學(xué)描述。
最后就是對(duì)上面的公式進(jìn)行求解了,這中間會(huì)用到拉格朗日乘子和 KKT 等條件,就不再繼續(xù)擴(kuò)展了,有興趣的同學(xué)可以查看周志華老師的《機(jī)器學(xué)習(xí)》支持向量機(jī)一篇,里面有非常詳細(xì)的推導(dǎo)過(guò)程。
SVM 擴(kuò)展
我們現(xiàn)在假設(shè)樣本數(shù)據(jù)是完全線性可分的,那么學(xué)習(xí)到的模型就可以稱之為硬間隔支持向量機(jī),即硬間隔就是指完全正確的分類,不存在錯(cuò)誤的情況。
但是在真實(shí)的世界中,數(shù)據(jù)往往都不是那么“干凈”的,存在異常數(shù)據(jù)是再正常不過(guò)了,此時(shí)就需要軟間隔。軟間隔就是指允許一部分?jǐn)?shù)據(jù)樣本分類錯(cuò)誤,從而使得訓(xùn)練的模型可以滿足絕大部分其他樣本。
還存在另外一種情況,就是非線性的數(shù)據(jù)集。我們前面討論的都是線性情況下的分類,那么對(duì)于非線性的情況,SVM 也是支持的,就是非線性支持向量機(jī)。
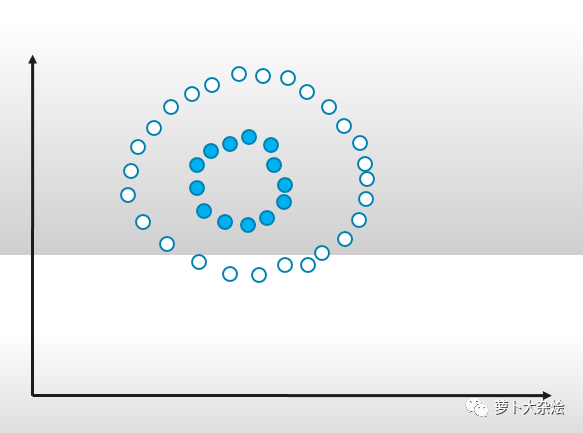
比如該類數(shù)據(jù)集,任何線性模型都沒(méi)有辦法處理,SVM 也是不可用的。此時(shí),我們就需要引入一個(gè)新的概念:核函數(shù)。它可以將樣本從原始的空間映射到一個(gè)更高緯度的空間中,從而使得在新的空間中樣本是線性可分的,這樣就可以繼續(xù)使用 SVM 來(lái)做分類了。
在非線性 SVM 中,核函數(shù)的選擇是影響 SVM 的最大因素。常用的核函數(shù)有線性核、多項(xiàng)式核、高斯核、拉普拉斯核,sigmoid 核等,或者是使用它們的組合核函數(shù)。通過(guò)這些核函數(shù)的轉(zhuǎn)換,我們就可以把樣本空間投射到新的高維度空間中。
SVM 實(shí)現(xiàn)多分類
SVM 本身是一個(gè)二值分類器,但是我們可以很方便的把它擴(kuò)展到多分類的情況,這樣就可以很好的應(yīng)用到文本分類,圖像識(shí)別等場(chǎng)景中。
擴(kuò)展 SVM 支持多分類,一般有兩種方法,OVR(one versus rest),一對(duì)多法;OVO(one versus one),一對(duì)一法。
OVR:對(duì)于 k 個(gè)類別發(fā)情況,訓(xùn)練 k 個(gè)SVM,第 j 個(gè) SVM 用于判斷任意一條數(shù)據(jù)是屬于類別 j 還是非 j。
舉個(gè)栗子:一組數(shù)據(jù) A,B,C,我們先把其中的一類分為1,其他兩類分為2,則可以構(gòu)造 SVM 如下:
樣本 A 為正集,B,C 為負(fù)集;
樣本 B 為正集,A,C 為負(fù)集;
樣本 C 為正集,A,B 為負(fù)集。
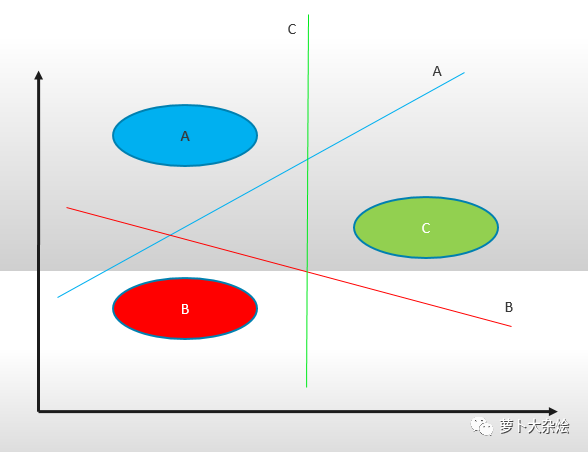
這種方法需要針對(duì) k 個(gè)分類訓(xùn)練 k 個(gè)分類器,分類的速度比較快,但是訓(xùn)練的速度較慢。當(dāng)新增一個(gè)分類時(shí),需要重新對(duì)分類進(jìn)行構(gòu)造。
OVO:對(duì)于 k 個(gè)類別的情況,訓(xùn)練 k * (k-1)/2 個(gè) SVM,每一個(gè) SVM 用來(lái)判斷任意一條數(shù)據(jù)是屬于 k 中的特定兩個(gè)類別中的哪一個(gè)。
相同的栗子:一組數(shù)據(jù) A,B,C,我們把任意兩類樣本之間構(gòu)造一個(gè) SVM,那么可以構(gòu)造如下:
分類器1,A,B;
分類器2,B,C;
分類器3,A,C。
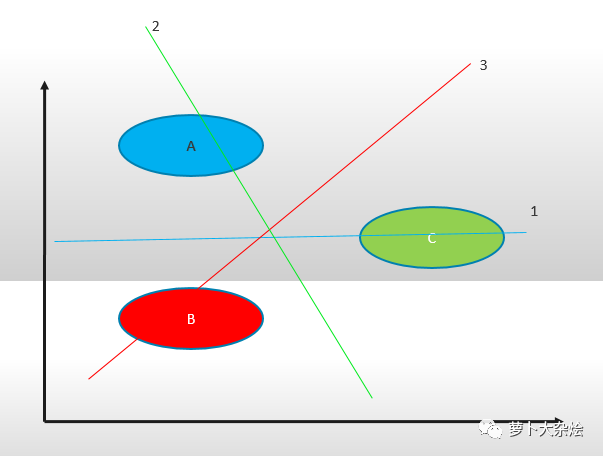
對(duì)于一個(gè)未知的樣本,每一個(gè)分類器都會(huì)有一個(gè)分類結(jié)果,記票為1,最終得票最多的類別就是未知樣本的類別。這樣當(dāng)新增類別時(shí),不需要重新構(gòu)造 SVM 模型,訓(xùn)練速度快。但是當(dāng) k 較大時(shí),訓(xùn)練和測(cè)試時(shí)間都會(huì)比較慢。
SVM 優(yōu)缺點(diǎn)
優(yōu)點(diǎn)
SVM 既可以用于分類,也可以用于回歸,學(xué)習(xí)能力強(qiáng),學(xué)習(xí)到的結(jié)果具有很好的推廣性。
SVM 是深度學(xué)習(xí)網(wǎng)絡(luò)出現(xiàn)之前,機(jī)器學(xué)習(xí)領(lǐng)域的絕對(duì)王者
SVM 可以很好的解決小樣本,高緯度問(wèn)題
缺點(diǎn)
對(duì)于參數(shù)調(diào)節(jié)和核函數(shù)的選擇很敏感
當(dāng)數(shù)據(jù)量特別大時(shí),訓(xùn)練很慢
總結(jié)
今天我們一起學(xué)習(xí)了 SVM 算法,可以說(shuō)它是機(jī)器學(xué)習(xí)領(lǐng)域必備的算法,沒(méi)有之一。
它本身是處理二值分類問(wèn)題的,但是同樣可以通過(guò)構(gòu)造多個(gè) SVM 分類器來(lái)靈活的處理多分類問(wèn)題。
我們還簡(jiǎn)單的推導(dǎo)了在線性可分的情況下 SVM 的數(shù)學(xué)公式,而對(duì)于非線性可分的數(shù)據(jù),我們需要引入核函數(shù),來(lái)映射原始數(shù)據(jù)到一個(gè)新的高緯度空間中,再進(jìn)行 SVM 構(gòu)建。