【關于 CNN】那些你不知道的事

貢獻者：天驕，小豬呼嚕，沐風，楊夕，芙蕖，李玲

 s

一、動機篇

• 全連接網絡：任意一對輸入與輸出神經元間都存在連接，現成稠密結構

• 局部特征存在相關性

二、CNN 卷積層篇

2.1 卷積層的本質是什么？

• 稀疏交互

• 動機：全連接網絡，任意一對輸入與輸出神經元間都存在連接，現成稠密結構

• 思路：卷積核尺度遠小于輸入維度，每個輸出神經元僅與前一層特定局部區(qū)域內的神經元存在連接

• 優(yōu)點：全連接層的 參數 為 mn；卷積層為 kn (m為輸入，n為輸出，k 為 卷積維度)

• 參數共享

• NN：計算每層輸出時，權值參數矩陣中每個元素只作用于每個輸入元素一次

• CNN：卷積核中每個元素將作用于每個局部輸入的特定位置上

• 思路：在同一模型的不同模塊中使用相同參數，為卷積運算的固有屬性

• 區(qū)別

• 物理意義：使卷積層具有平移不變性 (滿足 f(g(x)) = g(f(x)) 時，稱 f(x) 關于g 具有等變性)

2.2 CNN 卷積層與全連接層的聯系？

1. 卷積核中的權值每次滑動計算時只是局部連接，且在卷積列中的神經元共享參數——計算局部信息，而全連接層神經元的權值與所有輸入相連——計算全局信息。

2. 兩者都是采用的矩陣點積運算，具有相似的計算形式，能夠實現互相轉化。

1. 卷積——>全連接： 權重矩陣參數增大，權重補0，由于參數共享性質，在其中大部分塊中，存在大量相等參數。

2. 全連接——>全卷積： 將卷積核的尺寸設置為和輸入數據體的尺寸一致（NxWxHxC）。除第一層全連接外，其他通道數都為1，N表示本層神經元的個數，為一個提前設定的超參數，結果與初始的那個全連接層一致。

3. 一個深度卷積神經網絡模型通常由若干卷積層疊加若干全連接層組成，中間也包含各種非線性操作以及池化操作。卷積層的作用是從輸入數據中采集關鍵數據內容。全連接層在深度卷積神經網絡中的作用是將前面經過多次卷積后高度抽象的特征進行整合。最后一層作歸一化，然后輸出概率。卷積層提供了一個有意義、低維度且?guī)缀醪蛔兊奶卣骺臻g，然后全連接層在這個空間里學習一個非線性的方程。通俗的說，卷積層是特征提取器，全連接層執(zhí)行分類操作。

4. 全連接層可以視作一種特殊的卷積。考慮下面兩種情況：

1. (1) 特征圖和全連接層相連，AlexNet經過五次池化后得到7*7*512的特征圖，下一層全連接連向4096個神經元，這個過程可以看作有4096個7*7*512的卷積核和7*7*512的特征圖進行卷積操作，最終得到1*1*4096的特征圖，等價于全連接得到4096個神經元。

2. (2) 全連接層和全連接層相連，AlexNet的再下一層依然是4096個神經元，即4096個神經元和4096個神經元全連接，由(1)得到了1*1*4096的特征圖，本次全連接過程可以看作存在4096個1*1*4096的卷積核，依次和1*1*4096的特征圖進行卷積操作，等價于全連接。

2.3 channel的含義是什么？

在卷積神經網絡中，channel的含義是每個卷積層中卷積核的數量。卷積層的卷積個數就等于卷積層輸出的out_channels。這個值也與下一層卷積的in_channels相同。下面舉例說明。

如下圖，假設現有一個為 6×6×3 的圖片樣本，使用 3×3×3 的卷積核（filter）進行卷積操作。此時輸入圖片的 channels 為 3 ，而卷積核中的 in_channels 與 需要進行卷積操作的數據的 channels 一致（這里就是圖片樣本，為3）。

接下來，進行卷積操作，卷積核中的27個數字與分別與樣本對應相乘后，再進行求和，得到第一個結果。依次進行，最終得到 4×4的結果。

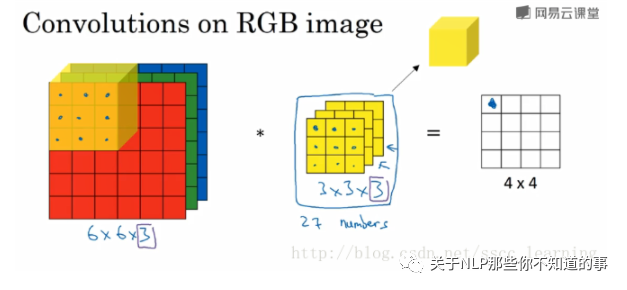
上面步驟完成后，由于只有一個卷積核，所以最終得到的結果為 4×4×1， out_channels 為 1 。

在實際應用中，都會使用多個卷積核。這里如果再加一個卷積核，就會得到 4×4×2 的結果。

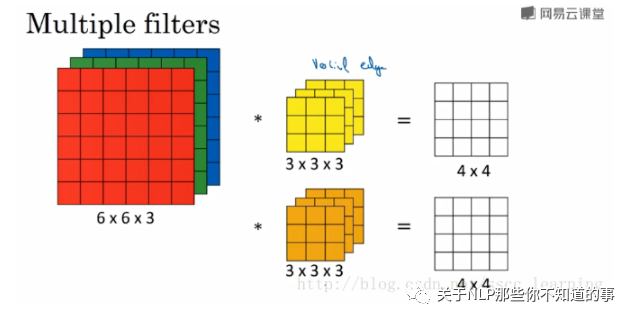
總結一下， channels 分為三種：

1. 最初輸入的圖片樣本的 channels ，取決于圖片類型，比如RGB；

2. 卷積操作完成后輸出的 out_channels ，取決于卷積核的數量。此時的 out_channels 也會作為下一次卷積時的卷積核的 in_channels；

3. 卷積核中的 in_channels ，就是上一次卷積的 out_channels ，如果是第一次做卷積，就是樣本圖片的 channels 。

三、CNN 池化層篇

3.1 池化層針對區(qū)域是什么？

池化層針對區(qū)域是非重疊區(qū)域。

3.2 池化層的種類有哪些？

• 均值池化

• 思路：對領域內特征值取平均

• 優(yōu)點：抑制由領域大小受限造成的估計值方差增大現象

• 特點：對背景的保留效果好

• 最大值池化

• 思路：取領域內最大值

• 優(yōu)點：抑制網絡參數誤差造成估計均值偏移問題

• 特點：更好提取紋理信息

3.3 池化層的作用是什么？

除降低參數量外，能夠保持對平移、伸縮、旋轉操作的不變性

3.4 池化層 反向傳播 是什么樣的？

• 動機：由于 Pooling 操作容易改變 feature map 的 尺寸大小，使得 Pooling 層不可導；

• 舉例說明：假定 22 的 池化，會生成 2222 = 16 個梯度，即梯度無法傳遞到對應的位置；

• 方法：將一個像素的loss (梯度) 傳遞給4個像素，且需要保證傳遞的 loss （梯度）總和不變。

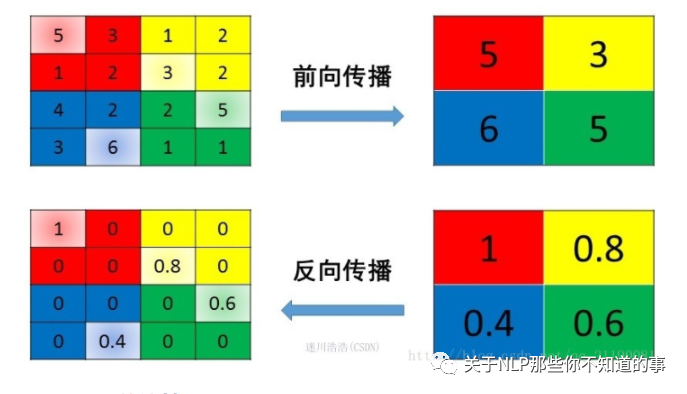
3.5 mean pooling 池化層 反向傳播 是什么樣的？

• mean pooling 前向傳播介紹：將 patch 中的值求平均來做 pooling;

• mean pooling 反向傳播介紹：將值的梯度均等分為 n*n 份 分配給上一層，以保證 池化 前后 梯度之和保存不變；

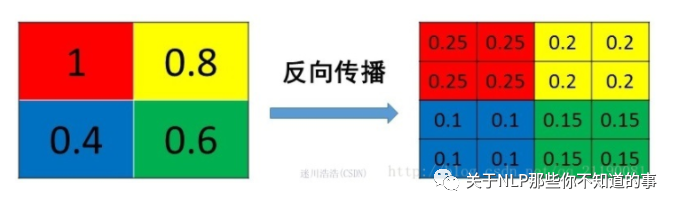
3.6 max pooling 池化層 反向傳播 是什么樣的？

• max pooling 前向傳播介紹：將 patch 中的值取 max 來做 pooling 結果 傳遞給下一層;

• max pooling 反向傳播介紹：把梯度直接傳給前一層 值最大的一個像素，而其他像素不接受梯度，也就是為0；

四、CNN 整體篇

4.1 CNN 的流程是什么？

• s1 輸入變長的字符串或單詞串

• s2 利用滑動窗口加池化的方式將原先的輸入轉化為固長的向量表示

4.2 CNN 的特點是什么？

CNN 能夠捕獲文本中的局部特征

4.3 卷積神經網絡為什么會具有平移不變性？

平移不變性：即目標在空間內發(fā)生平移，但是結果（標簽）不變

平移不變性=卷積+最大池化。卷積層具有平移等變性，池化層具有平移不變性。卷積神經網絡的平移不變性，是池化層賦予的。

如果一個函數滿足“輸入改變，輸出也以同樣的方式進行改變”這一性質，我們就說該函數是等變的（equivariant）。形式化地，如果函數$f(x)$與$g(x)$滿足$f(g(x))=g(f(x))$，我們就說$f(x)$對于變換$g$具有等變性。

卷積層具有平移等變性，也就是說卷積層對平移是敏感的，輸入的平移能等價地影響輸出。直觀地，如果把一張輸入圖像先平移后卷積，其結果與先卷積后平移效果是一樣的。如果我們移動輸入圖像中的物體，它的表示也會在輸出中移動同樣的量。

卷積層的參數共享（Parameter Sharing）特性使得卷積層具有平移等變性。參數共享是指在一個模型的多個函數中使用相同的參數。在傳統(tǒng)的神經網絡中，當計算一層的輸出時，權重矩陣的每個元素只使用一次。當它乘以輸入的一個元素后，就再也不會用到了。但是在卷積神經網絡中，卷積核的每一個元素都作用在輸入的每一個位置上。卷積運算中的參數共享保證了我們只需要學習一個參數集合，而不是對于每個位置都需要學習一個單獨的參數集合。

如果一個函數滿足“輸入改變，輸出不會受影響”這一性質，我們就說該函數是不變的（invariant）。形式化地，如果函數$f(x)$與$g(x)$滿足$g(x)=x'$且$f(x)=f(x')=f(g(x))$，我們就說$f(x)$對于變換$g$具有不變性。

池化層具有（近似）平移不變性，也就是說池化層對平移不敏感。不管采用什么樣的池化函數，當輸入做出少量平移時，池化能夠幫助輸入的表示近似不變。例如我們使用最大池化，只要變換不影響到最大值，我們的池化結果不會收到影響。對于一個卷積核來說，只有一個值的變動會影響到輸出， 其他的變換都不會造成擾動。平均池化的近似不變性就稍弱些。

局部平移不變性是一個很有用的性質，尤其是當我們關心某個特征是否出現而不關心它出現的具體位置時。

4.4 卷積神經網絡中im2col是如何實現的？

卷積的運算量十分巨大，如果將卷積運算轉化為矩陣運算，便能利用GPU來提升性能。

im2col全稱image to column（從圖像到矩陣），作用為加速卷積運算。即把包含批數量的4維數據轉換成2維數據。也就是將輸入數據降維，然后通過numpy的矩陣運算后得到結果，再將結果的形狀還原，從而通過用矩陣運算來代替for循環(huán)語句。

im2col將卷積核和卷積核掃過的區(qū)域都轉化為列(行)向量。舉個例子方便理解：

假設一個3*3卷積核為：

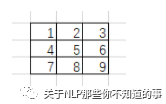
輸入圖像是5*5像素的單通道圖像：

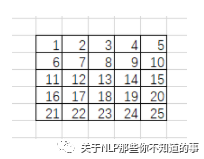
卷積核會鎖定3*3的滑動窗口：

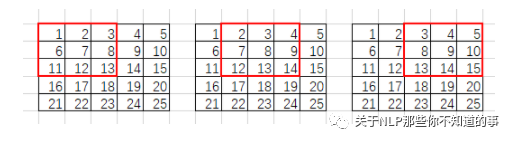
im2col會將每個滑動窗口內的像素轉為列向量：

就這樣轉化所有滑動窗口的列向量，將其拼接成9行的矩陣（行數與滑動窗口數目相關，列數則與卷積核大小相關）：

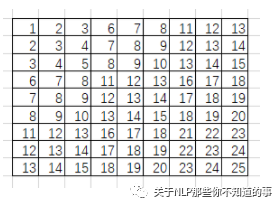
im2col還會將卷積核轉化為行向量：

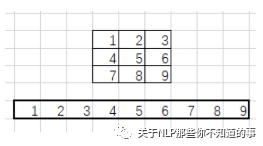
最后使用卷積核行向量乘以滑動窗口元素組成的矩陣：

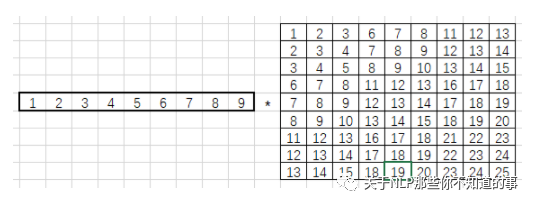
得到1*9的列向量，將其拼接成特征圖：

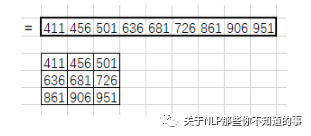
4.5 CNN 的局限性是什么？

1. 以CNN為代表的前饋神經網絡使用了條件獨立假設，其特征提取范圍受到限制；而循環(huán)神經網絡或者Attention機制的模型能夠看到序列整體的信息，因此對于序列建模任務，單純的CNN存在先天不足。

2. 卷積神經網絡的核心思想是捕捉局部特征。對于序列任務，比如文本來說，局部特征就是由若干單詞組成的滑動窗口（類似N-Gram）。卷積神經網絡的優(yōu)勢在于能夠自動地對N-Gram特征進行組合和篩選，獲得不同抽象層次的語義信息。

1. 解決方法：加入更多卷積層 -> 網絡深度增加 -> 參數量增大 -> 容易過擬合 -> 引入 Dropout 正則化 -> 引入超參數 -> 網絡龐大冗余，難以訓練

3. 使用CNN做序列任務的優(yōu)點在于其共享權重的機制，使得訓練速度相對較快；但是其最大的缺點在于CNN無法構建長距離依存關系。

4. 有許多研究者試圖改進CNN模型，使其能夠應用于序列任務。諸如用于句子語義建模的動態(tài)卷積神經網絡DCNN、可以在整個序列的所有窗口上進行卷積的時延神經網絡TDNN等。

五、Iterated Dilated CNN 篇

5.1 什么是 Dilated CNN 空洞卷積？

• 動機：

• 正常CNN 的 filler 作用于輸入矩陣連續(xù)位置，利用 卷積 和 池化 整合多尺度的上下文信息，導致分辨率損失

• pooling 會損失信息，降低精度，不加則導致感受野變小，學不到全局信息

• CNN提取特征的能力受到卷積核大小的限制，特別是對于序列問題，容易造成長距離依賴問題

• 介紹：Dilated Convolutions，翻譯為擴張卷積或空洞卷積。空洞卷積與普通的卷積相比，除了卷積核的大小以外，還有一個擴張率參數，主要用來表示擴張的大小，以及去掉 pooling。

• 空洞卷積與普通卷積的相同點：卷積核的大小是一樣的，在神經網絡中即參數數量不變，區(qū)別在于擴張卷積具有更大的感受野。感受野指的是特征圖上某個元素的計算受輸入圖像影響區(qū)域的范圍，即特征圖上神經元能夠“看到”的圖像范圍，例如3×3卷積核的感受野大小為9。

具體地，空洞卷積通過給卷積核插入“空洞”變相增加其大小。如果在卷積核的每兩個元素之間插入$D-1$個空洞，該卷積核的有效大小為$K'=K+(K-1)\times (D-1)$。其中$K$為原始卷積核大小，$D$稱為膨脹率(擴張率，dilation rate)。當$D=1$時卷積核為普通的卷積核。

例如下圖中

• (a) 普通卷積，1-dilated convolution，卷積核的感受野為3×3=9。

• (b) 空洞卷積，2-dilated convolution，卷積核的感受野為7×7=49。

• (c) 空洞卷積，4-dilated convolution，卷積核的感受野為15×15=225。

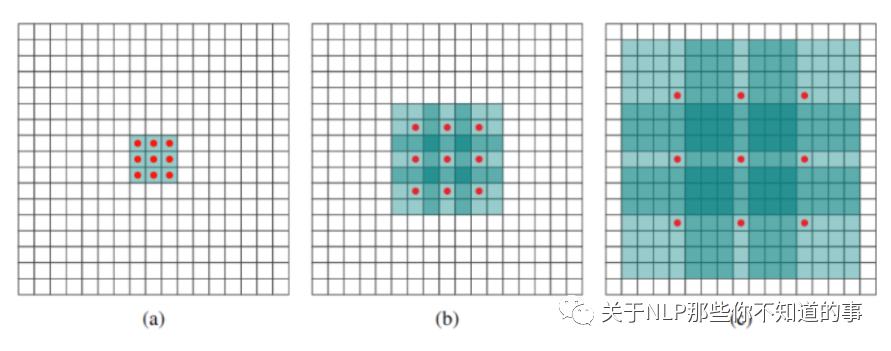
• 優(yōu)點：dilated width 會隨著層數增加而指數增加，層數 增加，參數量線性增長， 感受野 指數增加，可覆蓋全部信息

例如卷積核大小為3，步長為1，膨脹率為2的空洞卷積動態(tài)示意圖：

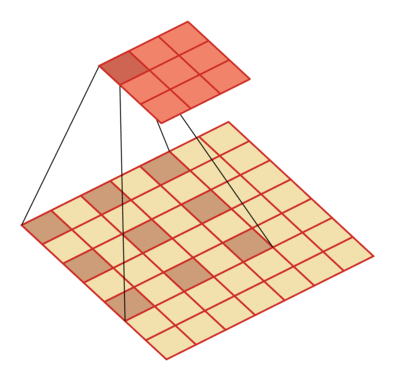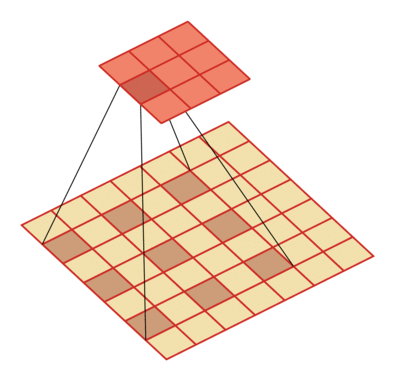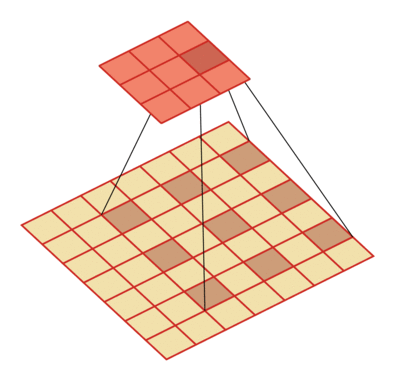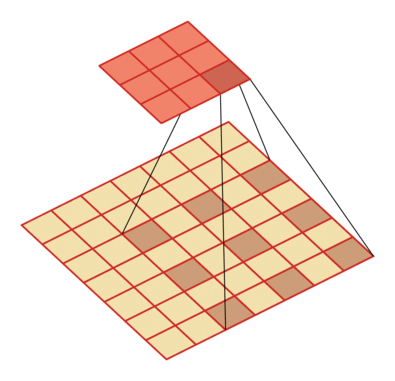
• 空洞卷積的作用

• 擴大感受野。如果希望增加輸出單元的感受野，一般可以通過增加卷積核大小、增加卷積層數，或在卷積前增加池化操作來實現。但是前兩者會增加參數數目，第三種方式會損失信息。空洞卷積就是一種增加感受野的同時不增加參數數量的方法。

• 捕獲多尺度上下文信息：在進行空洞卷積前，通過雙線性插值，對feature map進行上采樣之后，再進行空洞卷積，這樣可以在提高feature map的像素的同時，提取更多的全局信息

5.2 什么是 Iterated Dilated CNN？

• 思路：利用四個結構相同的 Dilated CNN 拼接起來，每個 block 里面 dilated width 為 1，1，2 的三層 DCNN，能夠捕獲更大感受野的信息

六、反卷積 篇

6.1 解釋反卷積的原理和用途？

1.反卷積原理

反卷積=上采樣=（轉置卷積+微步卷積）? 空洞卷積=一般意義上的廣義卷積（包含上采樣和下采樣）。

上采樣：在應用在計算機視覺的深度學習領域，由于輸入圖像通過卷積神經網絡(CNN)提取特征后，輸出的尺寸往往會變小，而有時我們需要將圖像恢復到原來的尺寸以便進行進一步的計算(e.g.:圖像的語義分割)，這個采用擴大圖像尺寸，實現圖像由小分辨率到大分辨率的映射的操作，叫做上采樣(Upsample)。

反卷積是一種特殊的正向卷積，先按照一定的比例通過補0來擴大輸入圖像的尺寸，接著旋轉卷積核，再進行正向卷積。

反卷積又被稱為Transposed(轉置) Convolution，其實卷積層的前向傳播過程就是反卷積層的反向傳播過程，卷積層的反向傳播過程就是反卷積層的前向傳播過程。因為卷積層的前向反向計算分別為乘 $C$ 和 $C^T$,而反卷積層的前向反向計算分別為乘 $C^T$ 和 $(C^T)^T$，所以它們的前向傳播和反向傳播剛好交換過來。

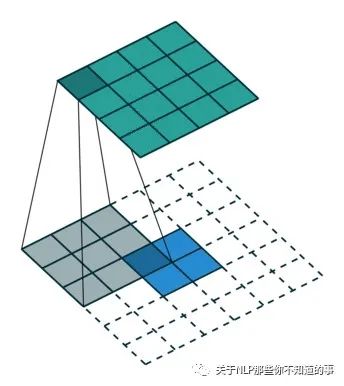
上圖展示一個反卷積的工作過程，乍看一下好像反卷積和卷積的工作過程差不多，主要的區(qū)別在于反卷積輸出圖片的尺寸會大于輸入圖片的尺寸，通過增加padding來實現這一操作，上圖展示的是一個strides(步長)為1的反卷積。下面看一個strides不為1的反卷積

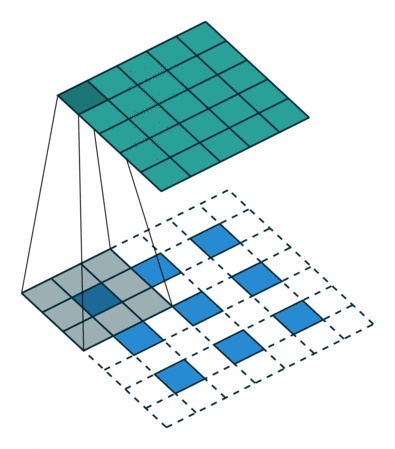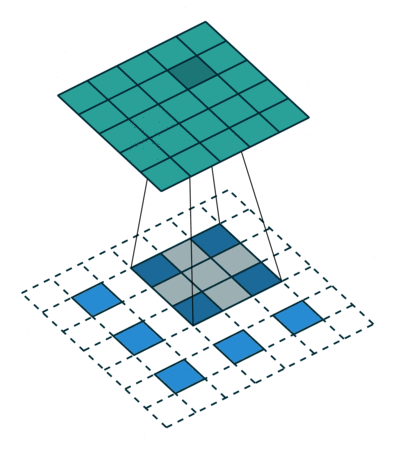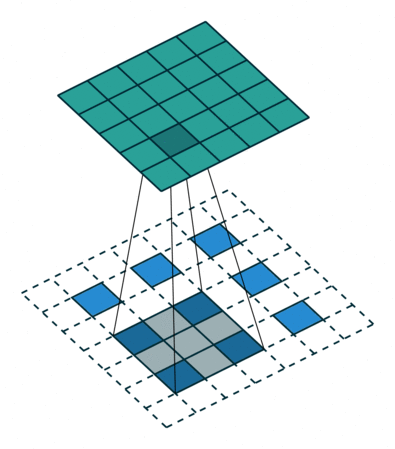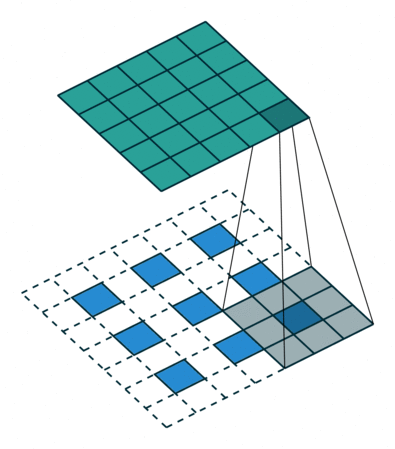
上圖中的反卷積的stride為2，通過間隔插入padding來實現的。同樣，可以根據反卷積的o、s、k、p參數來計算反卷積的輸出i，也就是卷積的輸入。公式如下：i=(o?1)?s+k?2?p。

2.作用

• 通過反卷積可以用來可視化卷積的過程

• 反卷積在GAN等領域中有著大量的應用。比如用GANs生成圖片，其中的generator和discriminator均采用深度學習，generator生成圖片過程中采用的就是反卷積操作（當然discriminator采用卷積對generator生成的圖片判別真?zhèn)危?/p>

• 將一些低分辨率的圖片轉換為高分辨率的圖片。

參考：

https://kknews.cc/code/zb2jr43.html

https://zhuanlan.zhihu.com/p/48501100

參考

1. 理解為什么要將全連接層轉化為卷積層

2. What do the fully connected layers do in CNNs?

3. CNN全連接層和卷積層的轉化

4. 【CNN】理解卷積神經網絡中的通道 channel

5. 萬字長文概述NLP中的深度學習技術